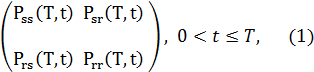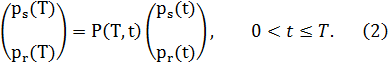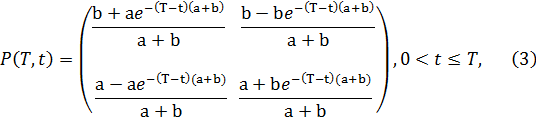PAPER:
The analysis of real data using a
stochastic dynamical system able to model spiky prices
Lorella Fatone, Francesca Mariani, Maria Cristina Recchioni, Francesco Zirilli
1.
Abstract
2.
Introduction
1.
The stochastic dynamical
system for spiky asset prices
2.
The filtering and the
calibration problems
3.
Numerical results (Animations 1, 2, 3, 4)
4.
References
1. Abstract
In this
paper we use filtering and maximum likelihood methods to solve a calibration
problem for a stochastic dynamical system used to model spiky asset prices. The
data used in the calibration problem are the observations at discrete times of
the asset price. The model considered has been introduced by V.A. Kholodnyi in [9], [10] and describes spiky asset prices as the product of two independent
stochastic processes: the spike process and the process that represents the
asset prices in absence of spikes. A Markov chain is used to regulate the
transitions between presence and absence of spikes. As suggested in [12] in a different context the calibration problem for this model is
translated in a maximum likelihood problem with the likelihood function defined
through the solution of a filtering problem. The estimated values of the model
parameters are the coordinates of a constrained maximizer
of the likelihood function. Furthermore, given the calibrated model, we develop
a sort of tracking procedure able to forecast forward asset prices. Numerical
examples using synthetic and real data of the solution of the calibration
problem and of the performance of the tracking procedure are presented. The
real data studied are electric power price data taken from the U.K. electricity
market in the years 2004-2009. After calibrating the model using the spot
prices, the forward prices forecasted with the tracking procedure and the
observed forward prices are compared. This comparison can be seen as a way to
validate the model, the formulation and the solution of the calibration problem
and the forecasting procedure. The result of the comparison is satisfactory. A
detailed exposition of the material summarized in this website can be found in [7]. A more general reference to the work of the authors and of their
coauthors in mathematical finance is the website: http://www.econ.univpm.it/recchioni/finance.
· The research
reported in this paper is partially supported by MUR - Ministero
Universitŕ e Ricerca (
· The numerical experience
reported in this paper has been obtained using the computing grid of ENEA
(Roma, Italy). The support and sponsorship of ENEA are gratefully acknowledged.
2. Introduction
A spike in an asset price is
an abrupt movement of the price followed by an abrupt movement of approximately
the same magnitude in the opposite direction. The modeling of spikes in asset
prices is a key problem in finance. In fact spiky prices are encountered in
several contexts such as, for example, in electric power prices and, more in
general, in commodity prices.
This website summarizes the work contained in [7]. In [7] the model introduced by V.A. Kholodnyi in [9], [10] to describe spiky prices is combined with some ideas introduced by the
authors and some coauthors to study calibration problems in mathematical
finance, see [12], [2], [3], [4], [5], [6], [1]. That is we introduce a stochastic dynamical system to model spikes in
asset prices and we study a calibration problem for the dynamical system
introduced. The method proposed to solve the calibration problem is tested
doing the analysis of data time series. We consider synthetic and real data.
The real data studied are electric power price data taken from the U.K.
electricity market in the years 2004-2009.
Following V.A. Kholodnyi
(see [9], [10]) we model spiky
asset prices as a stochastic process that can be represented as the product of
two independent stochastic processes: the spike process and the process that
describes the asset prices in absence of spikes. The spike process models
spikes in asset prices and it is either the multiplicative amplitude of the
spike during the spike periods or one during the regular periods, that is
during the periods between spikes. The second stochastic process of the Kholodnyi model describes prices in absence of spikes. This
last process has been chosen as a diffusion process. Finally a two-state Markov
chain in continuous time determines whether asset prices are in the spike
state, that is during a spike, or in the regular state, that is between spikes.
The model for spiky asset prices studied here depends
on five real parameters. Two of them come from the process that describes the
asset prices in absence of spikes, one of them comes from the spike process and
the last two parameters come from the two-state Markov chain used to model the
transitions between spike and regular states.
The calibration problem considered consists in
estimating these five parameters from the knowledge at discrete times of the
asset prices (observations of the spiky prices). That is the calibration
problem is a parameter identification problem or, more in general, is an
inverse problem for the stochastic dynamical system that models the asset
prices. This calibration problem is translated in a constrained optimization
problem for a likelihood function (maximum likelihood problem) with the
likelihood function defined through the solution of a filtering problem. The
likelihood function is defined using the probability density function
associated with the diffusion process modeling asset prices in absence of
spikes. This formulation of the calibration problem is inspired to the one
introduced in [12], in the study of
the Heston stochastic volatility model that has been
later extended to the study of several other calibration problems in
mathematical finance (see [2], [3], [6], [1]).
The filtering and the maximum likelihood problems
mentioned above are solved numerically. The resulting numerical solution of the
calibration problem determines the values of the (unknown) parameters that make
most likely the observations actually made. Note that in the processing of
numerical data to improve the robustness and the quality of the solution of the
calibration problem some preliminary steps are introduced in the optimization
procedure used to solve the calibration problem and the results obtained in
these preliminary steps are used to penalize the likelihood function obtained
from the filtering problem. That is the maximum likelihood problem originally
formulated in analogy to [12] is reformulated adding penalization terms to the
likelihood function and choosing an ad hoc initial guess for the optimization
procedure to improve the robustness and the quality of its solution. This
reformulated problem is solved numerically using a method based on a variable
metric steepest ascent method.
Furthermore, as a byproduct of the solution of the
filtering problem, we develop a tracking procedure that, given the calibrated
model, is able to forecast forward asset prices.
The method used to solve the calibration problem and the
tracking procedure are used to analyze data time series. Numerical examples of
the solution of the calibration problem and of the performance of the tracking
procedure using synthetic and real data are presented. The synthetic data are
obtained computing one trajectory of the stochastic dynamical system that
models spiky asset prices. We generate daily synthetic data for a period of two
years. The first year of data is generated with one choice of the model
parameters, the second year of data is generated with a different choice of the
model parameters. The second year of data is generated using as initial point
of the trajectory the last point of the first year of data. In the solution of
the calibration problem we choose as observation period a period of one year,
that is we use as data the daily observations corresponding to a time period of
one year, and we move one day at the time this observation period through the
two years of data. The calibration problem is solved for each choice of the
observation period. The two choices of the model parameters used to generate
the data and the time when the model parameters change value are reconstructed
satisfactorily by the calibration procedure. The real data studied are daily
electric power price data taken from the U.K. electricity market. These
electric power price data are spiky data. We choose the data of the calibration
problems considered as done above in the study of synthetic data extracting the
observation periods from a time series of five years (i.e. the years 2004-2009)
of daily electric power (spot) price data taken from the U.K. market. The
results obtained show that the model is able to establish a stable relationship
between the data time series and the estimated model parameter values. Note that
in the real data time series for each observation day we have the electric
power spot price and the associated forward prices observed that day for a
variety of delivery periods. That is for each spot price there is a set of
forward prices associated to it corresponding to different delivery periods.
Moreover in the calibration problem only spot prices are used as data. To
exploit this fact we proceed as follows. After calibrating the model using as
data the spot prices observed in the first three years of the data time series,
we use the calibrated model, the tracking procedure and the spot prices not
used in the calibration to forecast the forward prices associated to these last
spot prices. We compare the forward prices forecasted with the tracking procedure
with the observed forward prices. The comparison is satisfactory and
establishes the effectiveness of the model, the validity of the proposed
formulation and solution of the calibration problem and the quality of the
forecasted prices.
We
note that the model studied is too simplistic to be of practical value in
electricity markets. In fact our model is able to capture only one property of
the electric power prices: the presence of spikes. It does not consider, for
example, the mean-reverting property and the presence of weekly and season
cycles in electricity prices. This study aims to be a first attempt to solve,
with the strategy presented in Section 3, calibration
problems involving stochastic dynamical systems that can be used to describe
electric power prices. That is the methodology discussed in this paper can be
applied in the calibration of more sophisticated stochastic dynamical models
that can be used in electricity markets (see for example [11]).
A general reference to the work of the authors and of
their coauthors in mathematical finance is the website: http://www.econ.univpm.it/recchioni/finance.
The reader not interested in mathematical details may
jump to Section 5.
3. The stochastic dynamical system for spiky asset prices
Let us introduce a
stochastic dynamical system used to model spiky asset prices, see [9], [10]. In this model the spiky
prices are defined as the product of two stochastic processes: the spike
process and the process that describes asset prices in absence of spikes. As
said in the Introduction the transitions between spike and regular states are
regulated through a two state Markov chain in continuous time.
Let t be a real variable that denotes time, Mt,
t > 0, be the (continuous time) two-state (i.e. regular state, spike state)
Markov chain that regulates the transitions between spike and regular states
and let
|
be its 2×2 transition probability
matrix. Note that in (1) Pss(T,t) and Prs(T,t) denote the transition probabilities of going from the
spike state at time t respectively to the spike or to the regular state at time
T, and similarly Psr(T,t)
and Prr(T,t) denote
the transition probabilities of going from the regular state at time t
respectively to the spike or to the regular state at time T, ![]() .
.
Let 0 < t ≤T and pr(t), ps(t), pr(T), ps(T)
be respectively the probabilities of being in the regular state and in the
spike state at time t and at time T. We have:
|
In the time-homogeneous case it is possible to write
an explicit formula for the matrix P(T,t), t ≤T,
as a function of the parameters that define the generator of P(T,t), t ≤T. These parameters control the duration and
the frequency of the spikes, that is they control the expected lifetime of the
spike periods and the expected lifetime of the periods between spikes. It is
easy to see that in the case of a time-homogeneous Markov chain Mt,
t ≥ 0, the transition probability matrix P(T,t),
0 < t ≤T, is a function only of the difference T-t, and that we have [9]:
|
where a and b are non negative
real parameters. Moreover we assume that a, b are not both zero.
From now on in our model for spiky prices we always
assume that the two-state Markov chain Mt, t ≥ 0, is
time-homogeneous and, as a consequence, we assume that its transition
probability matrix P(T,t), 0 < t ≤T, is
given by (3).
The process that describes the asset prices in absence
of spikes is a diffusion process defined through the following stochastic
differential equation:
|
(4) |
|
where ![]() > 0 denotes the random variable that describes
the asset price in absence of spikes at time t, t > 0, µ, σ are
constants, Wt, t > 0, is the standard Wiener process, W0
= 0, dWt, t > 0, is its stochastic
differential and the random variable
> 0 denotes the random variable that describes
the asset price in absence of spikes at time t, t > 0, µ, σ are
constants, Wt, t > 0, is the standard Wiener process, W0
= 0, dWt, t > 0, is its stochastic
differential and the random variable ![]() > 0 is a given
initial condition. For simplicity we assume that the random variable
> 0 is a given
initial condition. For simplicity we assume that the random variable ![]() is concentrated in
a point with probability one and, with abuse of notation, we denote this point
with
is concentrated in
a point with probability one and, with abuse of notation, we denote this point
with![]() . Recall that µ is
the drift coefficient and σ > 0 is the volatility coefficient.
. Recall that µ is
the drift coefficient and σ > 0 is the volatility coefficient.
Equation (4) defines the asset price dynamics of the celebrated
Black-Scholes model. Note that the solution of (4), (5) is a Markov
process known as log-normal process. Note that several other Markov processes
different from the one defined through (4), (5) can be used to model asset price dynamics in absence
of spikes. For example instead than (4), (5) we can use one of the so called stochastic
volatility models that have been introduced recently in mathematical finance to
refine the Black-Scholes asset dynamics model.
Let us define the spike process ![]() , t ≥ 0, that
models the amplitude of the spikes in the asset prices. Let
, t ≥ 0, that
models the amplitude of the spikes in the asset prices. Let ![]() , t ≥ 0, be a
stochastic process made of independent positive random variables with given
probability density functions Σ(t,ξ),
ξ > 0, t ≥ 0. We assume that if the Markov chain Mt, t
≥ 0, is in the regular state then the spike process
, t ≥ 0, be a
stochastic process made of independent positive random variables with given
probability density functions Σ(t,ξ),
ξ > 0, t ≥ 0. We assume that if the Markov chain Mt, t
≥ 0, is in the regular state then the spike process ![]() , t ≥ 0, is
equal to one. If the Markov chain Mt, t ≥ 0, transits from the
regular state to the spike state at time τ, τ > 0, then the spike
process
, t ≥ 0, is
equal to one. If the Markov chain Mt, t ≥ 0, transits from the
regular state to the spike state at time τ, τ > 0, then the spike
process ![]() , t ≥ 0, is
equal to a value sampled from the random variable
, t ≥ 0, is
equal to a value sampled from the random variable ![]() during the entire time period beginning with t
= τ that the Markov chain Mt, t ≥ 0, remains in the spike
state. We assume that Mt, t ≥ 0, is in the regular state at
time t = 0 with probability one, so that the spike process
during the entire time period beginning with t
= τ that the Markov chain Mt, t ≥ 0, remains in the spike
state. We assume that Mt, t ≥ 0, is in the regular state at
time t = 0 with probability one, so that the spike process ![]() starts with
starts with ![]() = 1 with probability one. Let us observe that
in the case of spikes with constant amplitude λ > 1, the probability
density function Σ(t,ξ), = Σ(ξ), ξ > 0, t ≥
0, is the Dirac delta function δ(ξ-λ) with support in
ξ=λ, that is we have:
= 1 with probability one. Let us observe that
in the case of spikes with constant amplitude λ > 1, the probability
density function Σ(t,ξ), = Σ(ξ), ξ > 0, t ≥
0, is the Dirac delta function δ(ξ-λ) with support in
ξ=λ, that is we have:
|
(6) |
Finally we say that the spike process ![]() , t ≥ 0, is
in the spike state or in the regular state if the Markov chain Mt, t
≥ 0, is in the spike state or in the regular state respectively. In our model
for spiky prices we assume that the spikes have constant amplitude λ >
1, that is we assume (6).
, t ≥ 0, is
in the spike state or in the regular state if the Markov chain Mt, t
≥ 0, is in the spike state or in the regular state respectively. In our model
for spiky prices we assume that the spikes have constant amplitude λ >
1, that is we assume (6).
Let us define now the process that describes the asset
prices with spikes. Let us denote with St > 0 the random variable
that models the price (eventually) with spikes of the asset at time t ≥
0. We assume that the spike process ![]() , t ≥ 0, and
the process
, t ≥ 0, and
the process ![]() , t ≥ 0, that describes asset prices in
absence of spikes, are independent. Following [9], [10] we define the process
, t ≥ 0, that describes asset prices in
absence of spikes, are independent. Following [9], [10] we define the process ![]() , t ≥ 0, as
the product of the spike process
, t ≥ 0, as
the product of the spike process ![]() , t ≥ 0, and
of the process
, t ≥ 0, and
of the process ![]() , t ≥ 0, that
is:
, t ≥ 0, that
is:
|
Note that the process ![]() , t ≥ 0, for
spiky asset prices is in the spike state or in the regular state depending from
the fact that the spike process
, t ≥ 0, for
spiky asset prices is in the spike state or in the regular state depending from
the fact that the spike process ![]() , t ≥ 0, is
in the spike state or in the regular state respectively, or equivalently,
depending from the fact that the Markov chain Mt, t ≥ 0, is in
the spike state or in the regular state respectively.
, t ≥ 0, is
in the spike state or in the regular state respectively, or equivalently,
depending from the fact that the Markov chain Mt, t ≥ 0, is in
the spike state or in the regular state respectively.
In [9] it has been shown
that the process ![]() , t > 0, is able
to reproduce spikes in asset prices. This can be seen in Figure 1 where synthetic data sampled from
, t > 0, is able
to reproduce spikes in asset prices. This can be seen in Figure 1 where synthetic data sampled from ![]() , t > 0, are
shown. These synthetic data are those used in the numerical examples presented
in Section 5. Note that depending on the values of the
parameters defining the model, the trajectories of
, t > 0, are
shown. These synthetic data are those used in the numerical examples presented
in Section 5. Note that depending on the values of the
parameters defining the model, the trajectories of ![]() , t ≥ 0, can
exhibit a variety of behaviours. With the previous
choices for the spike process, the process that models prices in absence of
spikes and the continuous Markov chain
the model for spiky asset prices introduced in [9], [10] depends on five parameters,
that is: µ, σ, a, b, λ. The parameters µ and σ are those appearing in (4) and are relative
to the asset price model in absence of spikes, the remaining parameters are
relative to the spike process (i.e. λ) and to the Markov chain that
regulates the transitions between spike and regular states (i.e. a, b).
, t ≥ 0, can
exhibit a variety of behaviours. With the previous
choices for the spike process, the process that models prices in absence of
spikes and the continuous Markov chain
the model for spiky asset prices introduced in [9], [10] depends on five parameters,
that is: µ, σ, a, b, λ. The parameters µ and σ are those appearing in (4) and are relative
to the asset price model in absence of spikes, the remaining parameters are
relative to the spike process (i.e. λ) and to the Markov chain that
regulates the transitions between spike and regular states (i.e. a, b).
4. The filtering and the calibration problems
The parameters µ, σ, a, b, λ are grouped in the following vector:
|
(8) |
where the superscript T denotes
the transpose operator. The vector Θ is the unknown of the
calibration problem that must be determined from the data available. The
vectors Θ, describing admissible sets of parameter values, must
satisfy some constraints, that is we must have Θ ![]() M where:
M where:
|
(9) |
and R5 is the five
dimensional real Euclidean space.
The constraints contained in M express some
elementary properties of the model introduced in Section 3. Note that, when
necessary to take care of special circumstances, more constraints can be added
to M.
The data of the calibration problem are the
observation times: 0 = t0 < t1 < t2 <
... < tn < +∞, and the spiky
asset price ![]() observed at time ti,
i = 0,1,...,n, where
observed at time ti,
i = 0,1,...,n, where
![]() =
= ![]() =
= ![]() The observed price
The observed price ![]() is a positive real number that is understood
as being sampled from the random variables
is a positive real number that is understood
as being sampled from the random variables ![]() , i = 0,1,...,n.
Starting from these data we want to solve the following problems:
, i = 0,1,...,n.
Starting from these data we want to solve the following problems:
Calibration Problem: Find an estimate of the
vector Θ = (µ, σ, a, b, λ)T.
Filtering Problem (Forecasting Problem): Given the value
of the vector Θ = (µ, σ, a, b, λ)T
estimated forecast the forward asset prices.
Note that the prices ![]() , j = 0,1,...,n,
are called spot asset prices and that with forward asset prices we mean prices
“in the future”, that is, in our setting, we mean the forward prices at time ti associated to the spot price
, j = 0,1,...,n,
are called spot asset prices and that with forward asset prices we mean prices
“in the future”, that is, in our setting, we mean the forward prices at time ti associated to the spot price ![]() , i = n. These are
the prices at time ti of the asset with
delivery time t > ti, i = n. Let us point out that in correspondence of a spot
price we can forecast several forward prices associated to different delivery
periods. The delivery periods of interest are those actually used in real
markets, in fact for these delivery periods observed forward prices are
available and a comparison between observed forward prices and forecasted
forward prices is possible. In Section 5 in the analysis of
real data we consider (some of) the delivery periods used in the U.K.
electricity market in the years 2004-2009 and we make this comparison.
, i = n. These are
the prices at time ti of the asset with
delivery time t > ti, i = n. Let us point out that in correspondence of a spot
price we can forecast several forward prices associated to different delivery
periods. The delivery periods of interest are those actually used in real
markets, in fact for these delivery periods observed forward prices are
available and a comparison between observed forward prices and forecasted
forward prices is possible. In Section 5 in the analysis of
real data we consider (some of) the delivery periods used in the U.K.
electricity market in the years 2004-2009 and we make this comparison.
The calibration problem consists in estimating the
value of the vector Θ that makes “most likely” the observations.
The observations available at time t > 0 are denoted with:
|
Note that for simplicity we assume that the
transitions from regular state to spike state or vice versa happen at the
observation times.
Let p(![]() ,t|Ft,
Θ),
,t|Ft,
Θ), ![]() > 0, t > 0,
be the probability density function of the stochastic process
> 0, t > 0,
be the probability density function of the stochastic process ![]() at time t > 0
conditioned to the observations Ft and let pi(
at time t > 0
conditioned to the observations Ft and let pi(![]() ,t| Θ)
= p(
,t| Θ)
= p(![]() ,t|
,t|![]() , Θ),
, Θ), ![]() > 0, ti
< t ≤ti+1, be the probability density function of the
stochastic process conditioned to the observations made up to time t = ti, when ti
< t ≤ti+1, i = 0,1,...,n,
where we define tn+1 = +∞
> 0, ti
< t ≤ti+1, be the probability density function of the
stochastic process conditioned to the observations made up to time t = ti, when ti
< t ≤ti+1, i = 0,1,...,n,
where we define tn+1 = +∞
The probability density functions pi, i = 0,1,...,n-1, are the solutions of suitable initial
value problems for the Fokker-Planck equation associated to the Black-Scholes model and they can be written explicitly as an
integral with respect to the state variable of the product of the fundamental
solution of the Fokker-Planck equation associated to the Black-Scholes model with the appropriate initial conditions. See [7] for more details.
In order to measure the likelihood of the vector Θ
we introduce the following function:
|
It is worthwhile to note that definition (11) contains an important
simplification. In fact a more correct definition of the log-likelihood
function should be:
|
where ![]() =
= ![]() or
or ![]() =
= ![]() depending on whether at time ti+1 the
asset price is in the regular state or in the spike state respectively, i = 0,1,...,n-1. However, since when dealing with real
financial data the decision about the character of the state (regular or spike
state) of the observed prices is dubious, we prefer to adopt the definition (11) for the function.
In fact the choice made in (11), at the price of introducing some inaccuracy, avoids
the necessity of defining a (dubious) criterion to recognize regular and spike
states in order to evaluate the log-likelihood function. The validity of this
choice is supported by the fact that in the numerical experience shown in Section 5 the simplification introduced in (11) using
depending on whether at time ti+1 the
asset price is in the regular state or in the spike state respectively, i = 0,1,...,n-1. However, since when dealing with real
financial data the decision about the character of the state (regular or spike
state) of the observed prices is dubious, we prefer to adopt the definition (11) for the function.
In fact the choice made in (11), at the price of introducing some inaccuracy, avoids
the necessity of defining a (dubious) criterion to recognize regular and spike
states in order to evaluate the log-likelihood function. The validity of this
choice is supported by the fact that in the numerical experience shown in Section 5 the simplification introduced in (11) using ![]() instead of
instead of ![]() , i = 0,1,...,n-1,
is sufficient to obtain satisfactory results.
, i = 0,1,...,n-1,
is sufficient to obtain satisfactory results.
The solution of the calibration problem is given by
the vector Θ that solves the following optimization problem:
|
(13) |
Problem (13) is called maximum
likelihood problem. In fact the vector Θ*![]() M solution of (13) is the vector that
makes “most likely” the observations actually made. Problem (13) is an
optimization problem with nonlinear objective function and linear inequality
constraints. The optimization algorithm used to solve the maximum likelihood
problem (11), (13) is based on a variable metric steepest ascent method. The variable
metric technique is used to handle the constraints. See [7] for more details.
M solution of (13) is the vector that
makes “most likely” the observations actually made. Problem (13) is an
optimization problem with nonlinear objective function and linear inequality
constraints. The optimization algorithm used to solve the maximum likelihood
problem (11), (13) is based on a variable metric steepest ascent method. The variable
metric technique is used to handle the constraints. See [7] for more details.
Note that (11), (13) is one possible way of formulating the calibration
problem considered using the maximum likelihood method. Many other formulations
of the calibration problem are possible and legitimate. Moreover the
formulation of the calibration problem (11), (13) can be easily
extended to handle situations where we consider calibration problems associated
to data set different from the one considered here, such as, for example, data
set containing asset and option prices or only
option prices.
Numerical experiments have shown that the
(log-)likelihood function F(Θ) defined in (11) is a flat function. That is
there are many different vectors Θ in M that make likely
the data. In the optimization of objective functions with flat regions when
local methods, such as the steepest ascent method, are used to solve the
corresponding optimization problems, special attention must be paid to the
choice of the initial guess of the optimization procedure. That is in actual
computations a “good” initial guess Θ0 ∈ M is important to
find a “good” solution of the optimization problem (13). More specifically in the
problem considered here the use of good initial guesses of the volatility
σ and of the drift µ improves substantially the quality of the estimates
of all the parameters contained in the vector Θ. That is in the
solution of problem (13) the parameters µ and σ are the most “sensitive”
parameters of the vector Θ. For these reasons in order to improve
the robustness of the solution of problem (13) it is useful to introduce
some ad hoc steps that lead to a simple reformulation of the likelihood function (11) of the calibration problem
(13) and of the method used to solve problem (13). For simplicity we omit this
reformulation. See [7] for more details.
As a byproduct of the solution of the calibration
problem we obtain a technique to forecast forward asset prices. Let us consider
a filtering problem. We assume that the vector Θ solution of the
calibration problem associated to the data Ft = {![]() : ti ≤t}, t = tn
> 0 is known. From the knowledge of Θ = (µ, σ, a, b, λ)T at time t = tn
we can forecast the forward asset prices with delivery period Δt > 0 deep in the future and delivery time τn = tn+
Δt as follows:
: ti ≤t}, t = tn
> 0 is known. From the knowledge of Θ = (µ, σ, a, b, λ)T at time t = tn
we can forecast the forward asset prices with delivery period Δt > 0 deep in the future and delivery time τn = tn+
Δt as follows:
|
where E(·) denotes the
expected value of ·, and pr(τi), ps(τi) are,
respectively, the probabilities defined through the time-homogeneous Markov
chain Mt, t > 0, of
being in the regular and in the spike state at time t= τi, i = n (see (2)).
In the numerical experiments presented in Section 5 we use the following approximation:
|
|
E( |
Note that using formula (15) we
have implicitly assumed n > 9. In fact in the data time series considered in
Section 5 the average in time of the (spiky)
observations appearing in (15) gives a better approximation of the “spatial”
average E(![]() of the price without spikes than the
individual observation
of the price without spikes than the
individual observation ![]() made at time t = ti
of the spiky price. However the average in time of the observations
approximates the “spatial” average only if short time periods are used. This is
the reason why we limit the mean contained in (15) to the data corresponding to
ten consecutive observation times, that is corresponding to a period of ten
days when we process daily data as done in Section 5. Note that in (15) an average of spiky prices
is used to approximate the expected value of non spiky prices.
made at time t = ti
of the spiky price. However the average in time of the observations
approximates the “spatial” average only if short time periods are used. This is
the reason why we limit the mean contained in (15) to the data corresponding to
ten consecutive observation times, that is corresponding to a period of ten
days when we process daily data as done in Section 5. Note that in (15) an average of spiky prices
is used to approximate the expected value of non spiky prices.
5. Numerical results
The first numerical experiment
presented consists in solving the calibration problem discussed in Section 4 using synthetic data. This experiment does the analysis of a time
series of daily data of the spiky asset price during a period of two years. The
time series studied is made of 730 daily data of the spiky asset prices, that
is the prices ![]() at time ti,
i = 0,1,...,729. These data have been obtained
computing one trajectory of the stochastic dynamical system used to model spiky
asset prices defined in Section 3 looking at the
computed trajectory at time t = ti, i = 0,1,...,729, with ti-ti-1 =
1/365, i = 1,2,...,729, where we have chosen t0
= 0 and
at time ti,
i = 0,1,...,729. These data have been obtained
computing one trajectory of the stochastic dynamical system used to model spiky
asset prices defined in Section 3 looking at the
computed trajectory at time t = ti, i = 0,1,...,729, with ti-ti-1 =
1/365, i = 1,2,...,729, where we have chosen t0
= 0 and ![]() =
= ![]() =
= ![]() 20. We choose the
vector Θ that specifies the model used to generate the data equal
to Θ = (µ, σ, a, b, λ)T = Θ1 = (0.03,
0.3, 70, 1, 2) T in the first year of data (i.e. when t = ti,
i = 0,1,...,364), and equal to Θ = (µ, σ, a, b, λ)T = Θ2
= (0.1, 0.8, 150, 5, 4) T in the second year of data (i.e. when t = ti, i =
365,366,...,729). The data are generated using as initial value of the second
year the last datum of the first year. The synthetic data generated in this way
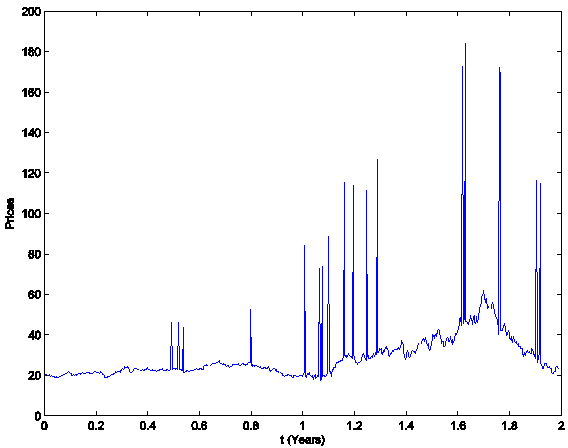
are shown in Figure 1. These data are spiky data
and the fact that the first year of data is generated using a different choice
of Θ than the choice made in the second year of data can be seen
simply looking at Figure 1.
20. We choose the
vector Θ that specifies the model used to generate the data equal
to Θ = (µ, σ, a, b, λ)T = Θ1 = (0.03,
0.3, 70, 1, 2) T in the first year of data (i.e. when t = ti,
i = 0,1,...,364), and equal to Θ = (µ, σ, a, b, λ)T = Θ2
= (0.1, 0.8, 150, 5, 4) T in the second year of data (i.e. when t = ti, i =
365,366,...,729). The data are generated using as initial value of the second
year the last datum of the first year. The synthetic data generated in this way
are shown in Figure 1. These data are spiky data
and the fact that the first year of data is generated using a different choice
of Θ than the choice made in the second year of data can be seen
simply looking at Figure 1.
We solve problem (13) with the ad hoc
procedure described in [7] using the data associated
to a time window made of 365 consecutive observation times, that is 365 days
(one year), and we move this window across the two years of data discarding the
datum corresponding to the first observation time of the window and inserting
the datum corresponding to the next observation time after the window. Note
that numerical experiments suggest that it is necessary to take a large window
of observations to obtain a good estimate the parameters a, b and λ. The
calibration problem is solved for each choice of the data time window applying
the procedure described in [7] and summarized in Section 4, that is it is solved 365 times. The 365 vectors Θ
constructed in this way are compared to the two choices of the model parameters
Θ used to generate the data. Moreover the time when Θ
changes from being Θ1 to being Θ2
is reconstructed. To represent the 365 vectors obtained solving the
calibration problem in correspondence to the 365 data time windows considered,
we associate to each reconstructed vector Θ ∈ R5 a point on a straight
line (see Figure 2). Let us explain how this correspondence is established. We
first represent the vectors Θ1 and Θ2
that generate the data as two points on the straight line mentioned above
having a distance proportional to ||Θ1- Θ2||*
measured in ||Θ1||* units, where ||Θ||*
=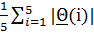 and Θ = (Θ(1),
Θ(2),...,Θ(5))T ∈ R5 and |·| denotes the absolute value of ·. We choose
the origin of the straight line to be the mid point
of the segment that joins Θ1 and Θ2.
In Figure 2 the diamond represents the vector Θ1 and the
square represents the vector Θ2. The unit length is ||Θ1||*.
The vectors (points) solution of the 365 calibration problems are represented
as (green or red) stars. A point P = Θ is plotted around Θ1
when the quantity ||Θ- Θ1||*/||Θ1||*
is smaller than the quantity ||Θ- Θ2||*/||Θ2||*,
otherwise the point P is plotted around Θ2. The distance
of the point P from Θ1 when P is plotted around Θ1
(or from Θ2 when P is plotted around Θ2)
is ||Θ1- Θ||* measured in ||Θ1||*
units (or ||Θ2- Θ||* measured in
||Θ1||* units). The point P = Θ
plotted around Θ1 is plotted to the right or to the left
of Θ1 according to the sign of the second component of Θ-
Θ1 (negative second component of Θ- Θ1
is plotted to the left of Θ1). Remind that the second
component of Θ is the volatility coefficient. A similar statement
holds for the points plotted around Θ2. The results
obtained in this experiment are shown in Figure 2 and Animations 1. In Figure 2 and Animations 1 the green stars represent
the solutions of the calibration problems associated to the first 183 data time
windows, that is the first “half” of data time windows, while the red stars
represent those associated to the second “half” of the data time windows (that
is the second 182 time windows). Figure 2 and Animations 1 show that the
points (vectors) obtained solving the calibration problems are concentrated on
two disjoint segments one to the left and one to the right of the origin and
that they form two disjoint clusters around Θ1 and Θ2.
That is, the solution of the 365 calibration problems corresponding to the 365
time windows described previously shows that two sets of parameters seems to
generate the data studied. This is really the case. Moreover, as expected, the
points of the cluster around Θ2 are in majority red
stars, that is they are in majority the points obtained by the analysis of data
time windows containing a majority of observations made in the second year (the
second “half” of the data time windows), and a similar statement holds for the
points of the cluster around Θ1 (in majority green
stars).
and Θ = (Θ(1),
Θ(2),...,Θ(5))T ∈ R5 and |·| denotes the absolute value of ·. We choose
the origin of the straight line to be the mid point
of the segment that joins Θ1 and Θ2.
In Figure 2 the diamond represents the vector Θ1 and the
square represents the vector Θ2. The unit length is ||Θ1||*.
The vectors (points) solution of the 365 calibration problems are represented
as (green or red) stars. A point P = Θ is plotted around Θ1
when the quantity ||Θ- Θ1||*/||Θ1||*
is smaller than the quantity ||Θ- Θ2||*/||Θ2||*,
otherwise the point P is plotted around Θ2. The distance
of the point P from Θ1 when P is plotted around Θ1
(or from Θ2 when P is plotted around Θ2)
is ||Θ1- Θ||* measured in ||Θ1||*
units (or ||Θ2- Θ||* measured in
||Θ1||* units). The point P = Θ
plotted around Θ1 is plotted to the right or to the left
of Θ1 according to the sign of the second component of Θ-
Θ1 (negative second component of Θ- Θ1
is plotted to the left of Θ1). Remind that the second
component of Θ is the volatility coefficient. A similar statement
holds for the points plotted around Θ2. The results
obtained in this experiment are shown in Figure 2 and Animations 1. In Figure 2 and Animations 1 the green stars represent
the solutions of the calibration problems associated to the first 183 data time
windows, that is the first “half” of data time windows, while the red stars
represent those associated to the second “half” of the data time windows (that
is the second 182 time windows). Figure 2 and Animations 1 show that the
points (vectors) obtained solving the calibration problems are concentrated on
two disjoint segments one to the left and one to the right of the origin and
that they form two disjoint clusters around Θ1 and Θ2.
That is, the solution of the 365 calibration problems corresponding to the 365
time windows described previously shows that two sets of parameters seems to
generate the data studied. This is really the case. Moreover, as expected, the
points of the cluster around Θ2 are in majority red
stars, that is they are in majority the points obtained by the analysis of data
time windows containing a majority of observations made in the second year (the
second “half” of the data time windows), and a similar statement holds for the
points of the cluster around Θ1 (in majority green
stars).
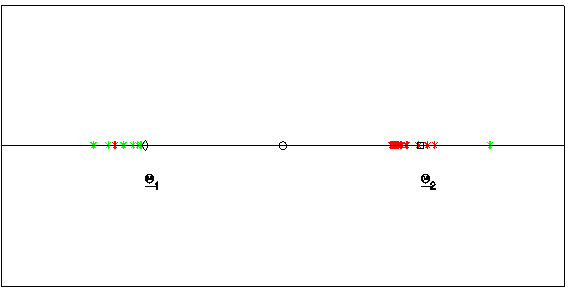
Figure 2: Reconstruction of
the parameter vectors Θ1 and Θ2.
Animation 1: click here to download a digital movie showing the points
determined solving the 365 calibration problems described above as a function
of the time window of the observations.
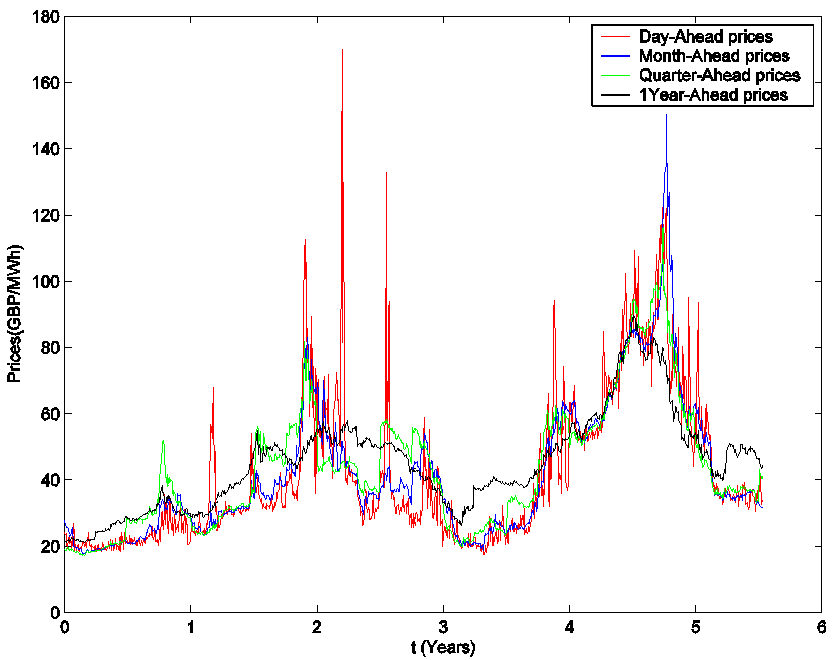
The second numerical experiment is performed using
real data. The real data studied are electric power price data taken from the
U.K. electricity market. These data are “spiky” asset prices. The data time
series studied is made of the observation times 0 = t0 < t1
< t2 < ... < tn = 1395
< +∞, (days), and of the spiky asset price ![]() observed at time ti, where
observed at time ti, where
![]() is the daily
electric power spot price (GBP/MWh), named Day-Ahead
price, i = 0,1,...,n. Excluding week-end days and
holidays this data time series corresponds to more than 5 years of daily
observations going from January 5, 2004 to July 10, 2009. Remind that GBP means
Great Britain Pound and that MWh means
Mega-Watt/hour.
is the daily
electric power spot price (GBP/MWh), named Day-Ahead
price, i = 0,1,...,n. Excluding week-end days and
holidays this data time series corresponds to more than 5 years of daily
observations going from January 5, 2004 to July 10, 2009. Remind that GBP means
Great Britain Pound and that MWh means
Mega-Watt/hour.
Moreover the data time series studied in
correspondence of each spot price contains a series of forward prices
associated to it for a variety of delivery periods. These prices include:
forward price 1 month deep in the future (Month-Ahead price), forward
price 3 months deep in the future (Quarter-Ahead price), forward price 4
months deep in the future (Season-Ahead price), forward price 1 year
deep in the future (One Year-Ahead price). These forward prices are
observed each day ti and the forward
prices observed at time ti are associated
to the spot price ![]() , i = 0,1,...,1395.
The spot and the forward prices contained in the data time series mentioned
above are shown in Figure 3.
, i = 0,1,...,1395.
The spot and the forward prices contained in the data time series mentioned
above are shown in Figure 3.
Figure 3: The U.K. electric
power price data.
The observed electric power prices generate data time
series with a complicated structure. The stochastic dynamical system studied in
this paper does not pretend to fully describe the properties of the electric
power prices. Indeed it is able to model only one property of these prices: the
presence of spikes. In addition the electricity prices have many other properties, for example, they are mean reverting and have
well defined periodicity, that is they have diurnal, weekly and seasonal
cycles. A lot of specific models incorporating (some of) these features are
discussed in the literature, see for example [11].
Let us begin performing the analysis of these data
using the model introduced in Section 3. The first
question to answer is: the model for spiky prices presented in Section 3 is an adequate model to analyze the time series of the spot prices? We
answer to this question analyzing the relationship between the data and the
model parameters established through the solution of the calibration problem.
Let us begin showing that the relation between the data and the model
parameters established through the calibration problem is a stable
relationship. We proceed as follows. We have more than 5 years of daily
observations. We apply the calibration procedure to the data corresponding to a
window of 257 consecutive observation times. Note that 257 is approximately the
number of working days contained in a year and remind that we have data only in
the working days. We move this window through the data time series discarding
the datum corresponding to the first observation time of the window and adding
the datum corresponding to the next observation time after the window. In this
way we have 1396-257=1139 data windows and for each one of these data windows
we solve the corresponding calibration problem. The calibration problems are
solved using the optimization procedure (including the ad hoc steps) described
in [7]. The reconstructions of the parameters obtained
moving the window along the data are shown in Figures
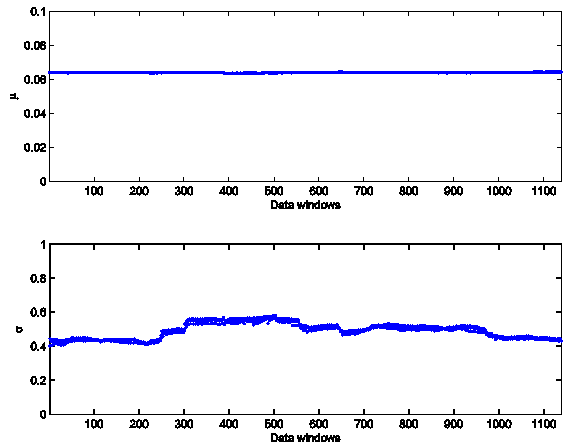
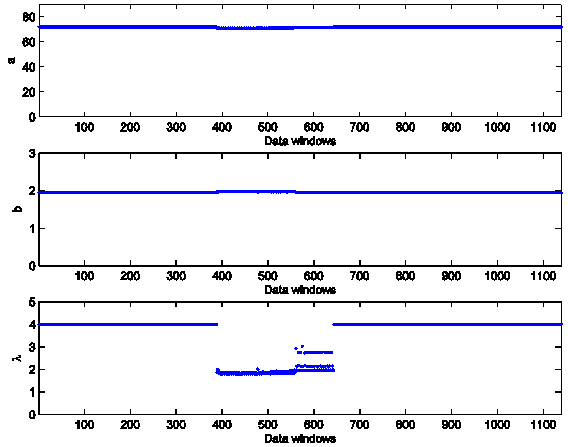
4, 5. In Figures 4, 5 the abscissa represents the data window used to
reconstruct the model parameters numbered in ascending order according to the
order in time of the first day of the window. Figures 4, 5 show
that the model parameters, with the exception of λ, are approximately
constant functions of the data window. The parameter λ reconstructed shown
in Figure 5 is
a piecewise constant function. These findings support the idea that the model
and the formulation of the calibration problem presented respectively in Section 3 and Section 4 are adequate to interpret the data. In fact
they establish a stable relationship between the data and the model parameters
as shown in Figure 4 and 5.
Figure 4: Reconstruction of
the parameters of the Black-Scholes model: µ, σ.
Figure 5: Reconstruction of
the parameters used to model the spikes: a, b, λ.
In the analysis of the real
data time series the second question to answer is: the solution of the
calibration problem and the tracking procedure introduced in Section 4 can be used to forecast forward prices? To answer this question we
compare the observed and the forecasted forward prices. We apply the
calibration procedure to a data window made of the first three years of
consecutive observations of the spot price taken from the data time series
shown in Figure 3 and we use the solution of the calibration problem found and formulae (14), (15) to calculate the forecasted
forward prices associated to the spot prices of the data time series not
included in the data window mentioned above used in the calibration problem. In
Figures 6, 7, 8 and Animations 2, 3, 4 the forward electric power prices forecasted are
shown and compared to the observed forward electric power prices. The Animations 2, 3, 4 show respectively
the quality of the forecasted forward prices 1 month, 3 months and 1 year deep
in the future. In Figures 6, 7, 8 and Animations 2, 3, 4 the abscissa is the day of the spot price associated
to the forward prices computed. The abscissa of Figures 6, 7, 8 and Animations 2, 3, 4 is coherent with the abscissa of Figure 3. Table 1
summarizes quantitatively the results shown in Figures 6, 7, 8 and Animations 2, 3, 4 and gives the average relative error eforward prices committed using
the forecasted forward prices, that is the average relative error committed
approximating the observed forward prices with the forecasted forward prices.
Table 1, Figures 6, 7, 8 and Animations 2, 3, 4 show the high
quality of the forecasted forward prices answering the second question posed
about the analysis of the data time series in the affirmative.
|
eforward
prices |
|
|
30
(Month-Ahead prices) |
0.0796
|
|
90
(Quarter-Ahead prices) |
0.1160
|
|
365
(One Year-Ahead prices) |
0.2183 |
Table 1: Average relative
errors of the forecasted forward electric power prices when compared to the
observed forward prices.
We can conclude that the data analysis presented shows
that the model introduced to describe spiky prices, the formulation of the
calibration problem and its numerical solution presented in this paper have the
potential of being tools of practical value in the analysis of data time series
of spiky prices.
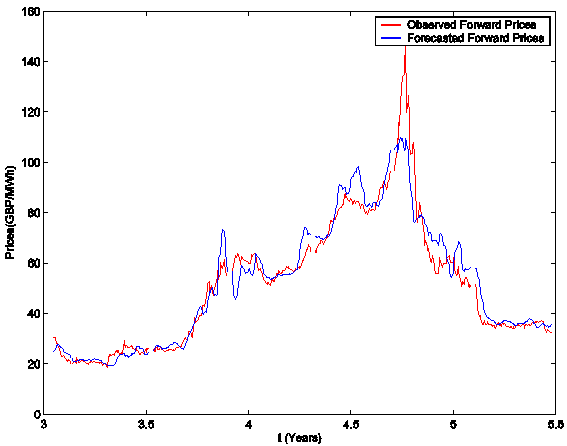
Figure 6: Month-Ahead prices.
Animation 2: click here to download a
digital movie showing
the quality of the forecasted Month-Ahead prices.
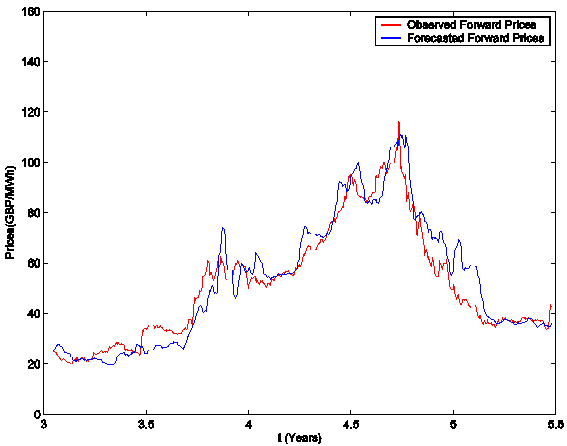
Figure 7: Quarter-Ahead
prices.
Animation 3: click here to download a digital movie
showing the quality of the forecasted Quarter-Ahead prices.
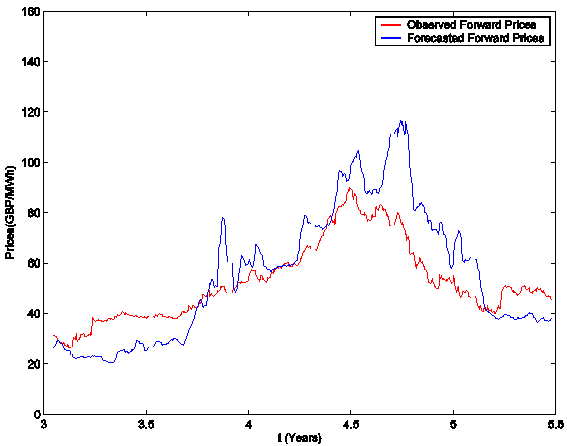
Figure 8: One Year-Ahead
prices.
Animation 4: click here to download a digital movie
showing the quality
of the forecasted One Year-Ahead prices.
6. References
[1] P.Capelli, F.Mariani, M.C.Recchioni, F.Spinelli, F.Zirilli,
“Determining a stable relationship between hedge fund index HFRI-Equity and
S&P 500 behaviour, using filtering and maximum
likelihood”, Inverse Problems in Science and Engineering, 18, pp.
93-109, 2010. (http://www.econ.univpm.it/recchioni/finance/w8).
[2] L. Fatone,
F.Mariani, M.C.Recchioni, F.Zirilli, “Maximum likelihood estimation of the parameters
of a system of stochastic differential equations that models the returns of the
index of some classes of hedge funds”, Journal of Inverse and Ill Posed
Problems, 15, pp. 493-526, 2007. (http://www.econ.univpm.it/recchioni/finance/w5).
[3] L.Fatone,
F.Mariani, M.C.Recchioni, F.Zirilli, “The calibration of the Heston
stochastic volatility model using filtering and maximum likelihood methods”, in
Proceedings of Dynamic Systems and Applications, G.S.Ladde,
N.G.Medhin, Chuang Peng, M.Sambandham Editors, Dynamic Publishers, Atlanta, USA, 5,
pp. 170-181, 2008. (http://www.econ.univpm.it/recchioni/finance/w6).
[4] L.Fatone,
F.Mariani, M.C.Recchioni, F.Zirilli, “An explicitly solvable multi-scale stochastic
volatility model: option pricing and calibration”, Journal of Futures
Markets, 29(9), pp. 862-893, 2009. (http://www.econ.univpm.it/recchioni/finance/w7).
[5] L.Fatone,
F.Mariani, M.C.Recchioni, F.Zirilli, “Calibration of a multiscale
stochastic volatility model using as data European option prices”, Mathematical
Methods in Economics and Finance, 3,
pp. 49-61, 2008.
[6] L.Fatone,
F.Mariani, M.C.Recchioni, F.Zirilli, “The analysis of real data using a multiscale
stochastic volatility model”, European Financial Management, doi: 10.1111/j.1468-036X.2010.00584.x, (2011). (http://www.econ.univpm.it/recchioni/finance/w9).
[7] L.Fatone,
F.Mariani, M.C.Recchioni, F.Zirilli, “The analysis of real
data using a stochastic dynamical system able to model spiky prices”,
Journal of Mathematical Finance, 2, pp. 1-12, 2012.
[8] J.H.Hull,
Options, Futures, and Other Derivatives, 7th Edition, Pearson Prentice
Hall, London, 2008.
[9] V.A. Kholodnyi,
“Valuation and hedging of European contingent claims on power with spikes: A
non-Markovian approach”, Journal of Engineering
Mathematics, 49(3), pp. 233-252, 2004.
[10] V.A. Kholodnyi, “The non-Markovian
approach to the valuation and hedging of European contingent claims on power
with scaling spikes”, Nonlinear Analysis: Hybrid Systems, 2, pp.
285-304, 2008.
[11] C.R. Knittel, M.R. Roberts, “An empirical examination of restructured electricity prices”,
Energy
Economics, 27, pp. 791-817, 2005.
[12] F.Mariani,
G.Pacelli, F.Zirilli,
“Maximum likelihood estimation of the Heston
stochastic volatility model using asset and option prices: an application of
nonlinear filtering theory”, Optimization Letters, 2, pp.
177-222, 2008.