 |
Lorella Fatone1, Marco Giacinti2, Francesca Mariani3,
Maria Cristina Recchioni2, Francesco Zirilli4
We propose parallel algorithms (named Application 1 and Application 2) implemented in CUDA subroutines ready to run on Graphics Processing Units (GPUs) to price two kinds of financial derivatives, that is: continuous barrier options and realized variance options. The really satisfactory parallel performances of these subroutines are mainly due to two reasons: the mathematical treatment of the problems considered that leads to pricing formulae very well suited for GPU parallel computing and the flexibility of CUDA language that makes possible to implement parallel algorithms to exploit these formulae. The analysis of the parallel performance on a GPU of the CUDA implementation of these algorithms shows that the use of GPU computing can be of great benefit in financial applications. The use of parallel computing has gained importance in finance in the last decades due to the fact that the speed of the decision making process is a key success factor in the financial markets operations. The decision making process in the financial institutions (banks, insurance companies, hedge funds, ...) often involves the evaluation of a huge number of contracts of the same type varying the values assigned to some of the parameters that define the contracts and/or the models used to price them (such as, for example, strike price, maturity time, volatility, drift). This is a feature of the decision making process in the financial institutions very well suited for parallel and/or distributed computing. Moreover often the evaluation of an individual contract is done using Monte Carlo methods or reduces to the evaluation of an integral via numerical quadrature. These kinds of computation are also very well suited for parallel and /or distributed computing.
The work presented here is the CUDA implementation of two algorithms that exploit pricing formulae derived in [3] (Application 1, barrier options) and in [2] (Application 2, realized variance options). A more detailed version of the work summarized here is presented in [1].
A C++ implementation of numerical methods that evaluate the pricing formulae derived in [3], [2] is available as two subroutines of the QuantLib software library (http://quantlib.org/index.shtml) respectively in the websites:
http://quantlib.org/reference/class_quant_lib_1_1_perturbative_barrier_option_engine.html. .
and
http://quantlib.org/reference/class_quant_lib_1_1_integral_heston_variance_option_engine.html
where respectively the problem of pricing barrier options and realized variance options is considered. These C++ subroutines do not make use of parallel computing. A grid enabled version of these C++ subroutines and of some other QuantLib subroutines [5] based on the use of a middleware software product of Platform Computing Inc., Toronto, (http://www.platform.com/) known as Symphony DE application can be downloaded from the website:
http://www.ceri.uniroma1.it/ceri/zirilli/w5/.
A more detailed version of the work summarized here is presented in [1]. A general reference to the work of some of the authors and of their coauthors in mathematical finance is the website: http://www.econ.univpm.it/recchioni/finance/ .
In the numerical experiments discussed below the GPU used is the NVIDIA "GeForce GTX 285" having 30 multiprocessors for a total of 240 cores (each core is a GPU processing unit) and the CPU used is an Intel core 2 duo E8500 3.18 GHz. The GPU speed up factors presented are computed as the ratio TCPU/TGPU,p where p is the number of processing units (i.e. cores) of the GPU used, TGPU,p is the (wall clock) execution time of the parallel algorithm on p processing units of the GPU and TCPU is the (wall clock) execution time of the corresponding sequential algorithm on the CPU. The subroutines executed on the CPU are the QuantLib C++ subroutines mentioned above. The results presented are obtained using p=240, that is in the numerical experiments all the 240 cores of the GPU are used in the computation. Here we limit our attention to the parallel performance of the codes on the GPU, a more complete analysis that includes the study of the accuracy of the results obtained can be found in [1], [2], [3].
Application 1: Barrier options
A continuously monitored up and out single barrier option is an option that is terminated when the price of the underlying asset goes above a fixed trigger (i.e. the barrier) within the lifetime of the option contract [6].
Application 1 prices a barrier option in the Black and Scholes framework with time dependent parameters evaluating numerically a truncated series expansion of the option price. The first three terms of this series expansion have been written as expressions containing integrals of explicitly known integrands that involve some elementary and non elementary transcendental functions (see [1], [3], [5] and this website http://www.econ.univpm.it/recchioni/finance/w3 for further details). Application 1 evaluates numerically these three terms in a way well suited for GPU computing [1].
The CUDA implementation of Application 1 is rather complex. In fact in Application 1 the option value is approximated using a truncation of a perturbative series expansion, that we denote with P0+P1+P2 where P0, P1, P2 are respectively the zeroth, first and second order terms of the series expansion considered (see [1], [3] for details). Let N1 and N2 be positive integers. The computation of the zero-th order term P0 involves only the evaluation of elementary functions (such as, for example, univariate normal distributions). The computation of the first order term P1 involves the evaluation of a one dimensional integral of bivariate normal distributions. This integral is approximated using a numerical quadrature formula with N1 quadrature nodes. The computation of the second order term P2 involves the evaluation of multidimensional integrals of bivariate and trivariate normal distributions that are approximated using a numerical quadrature formula with N1·N2 quadrature nodes. The evaluation of the term P2 is the most demanding part of the computation and for this reason has been implemented in CUDA and is executed on the GPU using parallel computing. The sum P0+P1 is always computed on the CPU. In fact when N1, N2 are large enough to guarantee accurate approximations of the quantities computed the numerical experience shows that the (wall clock) execution time required to compute the approximation of P0+P1 on the CPU is always negligible with respect to the (wall clock) execution time required to compute the approximation of P2 on the GPU. Hence in the CUDA implementation of Application 1 the use of the GPU is limited to the computation of the second order term P2 . In fact the GPU implementation of the computation of P0+P1 will not change significantly the time required to compute the approximation of the barrier option price given by P0+P1+P2. This way of doing is called "hybrid CUDA implementation" of the computation P0+P1+P2.
A test problem consisting in pricing a barrier option considered in [1], [3] is studied. The results obtained are shown in Table 1 where the (wall clock) execution times are shown. Table 1 shows that the "hybrid CUDA implementation" (t*GPU,240) of the computation of P0+P1+P2 (i.e. P0+P1 computed on the CPU and P2 computed on the GPU) outperforms the CPU implementation (t*CPU) of the same computation in term of (wall clock) execution time. Table 1 shows a speed up factor belonging to the interval [15,20] that slightly increases when the number N1·N2 increases. Moreover Table 1 shows that using parallel computing on the GPU we can compute the value of the barrier option considered in an affordable time (a few minutes) even when the number of quadrature nodes employed is large while the same computation on the CPU will require a few hours. Note that when N1, N2 are chosen as in Table 1 and N1·N2 is of order 106 in the example considered in [1], [3] at least six, seven correct significant digits are guaranteed in the numerical quadratures.
 |
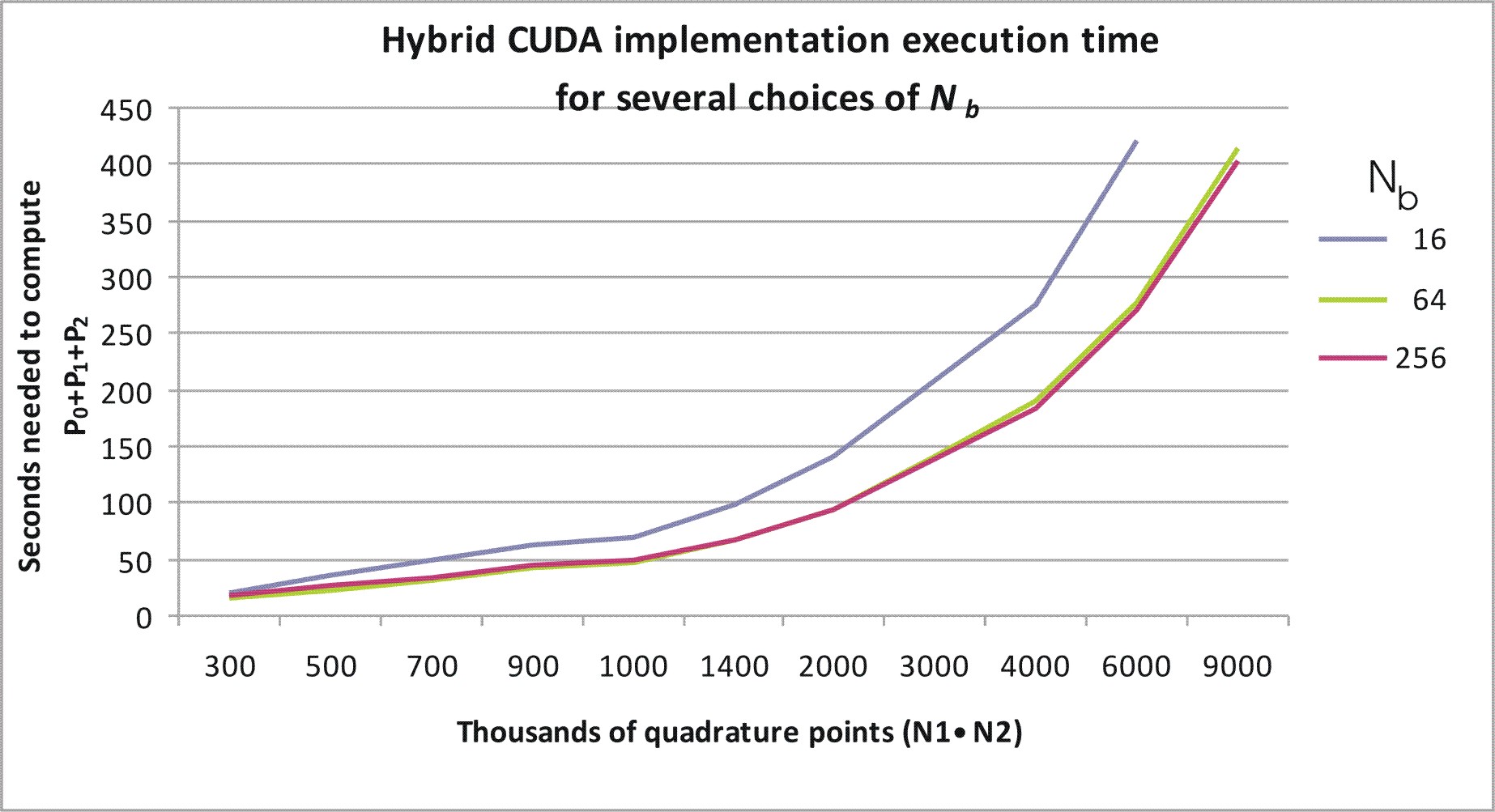
Let n1, n2 be positive integers, we must mention the fact that when one tries to compute at once on the GPU n1·n2 function values of the integrand function of the two dimensional integrals that define P2 and n1, n2 are large enough the GPU encounters a so called "watchdog timer" error. This error consists in the fact that the operating system stops the GPU functioning when the GPU remains out of the control of the operating system (lack of activity for the operating system) for a too long time. To avoid the GPU crash induced by the "watchdog timer" error we have divided the computation of the sum of the addenda contained in the numerical approximation of the integrals that define P2 in blocks of size Nb, that is we have split the computation partitioning the addenda using a block matrix of dimension N1·N2/Nb and each block Mk,m, k = 1,2,╝,N1, m = 1,2,╝N2/Nb, is made of 1·Nb addenda. These blocks are distributed between the GPU cores to be processed. Note that, for simplicity, we are assuming that N2/Nb is an integer. Roughly speaking, for k = 1,2,╝,N1, m = 1,2,╝N2/Nb the computation of the sum of the addenda contained in each block Mk,m is assigned to a GPU core and each core to perform its duty activates and executes a certain number of threads (in our numerical experience up to 512 threads). In our implementation Nb is the number of threads activated by each core. The optimal number of threads that each core must activate and execute to carry out the computation efficiently depends on the total numbers of blocks N1·N2/Nb. In fact the number of threads activated and executed by each core must be large enough to take the GPU busy but not so large to clog (to block) it due to the "watchdog timer" error. Figure 2 shows the (wall clock) execution time as a function of N1·N2 when N1, N2 are chosen as in Table 1 for several choices of Nb. We note that the choices Nb =64 and Nb =256 perform well.
|
N1 | N2 | t*CPU (sec) | t*GPU,240 (sec) | Speedup t*CPU/ t*GPU,240 |
|
1000 | 300 | 253.08 | 16.77 | 15.09 |
| 1000 | 500 | 424.94 | 25.09 | 16.93 |
| 1000 | 1000 | 849.88 | 48.45 | 17.54 |
| 1000 | 2000 | 1699.76 | 93.76 | 18.12 |
| 1500 | 2000 | 2549.64 | 139.68 | 18.25 |
| 2000 | 2000 | 3405.80 | 185.52 | 18.35 |
| 2000 | 3000 | 5099.28 | 273.96 | 18.61 |
| 3000 | 3000 | 7720.03 | 409.55 | 18.85 |
It is known that the most effective GPU computations make use of the so called "inline" compiler directives. However Application 1 cannot be implemented using the "inline" compiler directives on the GPU that we are using in our experiments since in the case of Application 1 the execution of the subroutine calls in the GPU core from where they originate that is required by the "inline" compiler directives saturates the RAM memory available to the individual GPU core. Therefore the CUDA implementation of Application 1 has been realized using the "noinline" compiler directives. This choice limits the parallel performance of the code. However, as shown in Table 1, the performance of the hybrid CUDA implementation of the computation of P0+P1+P2 with respect to the CPU implementation of the same computation in terms of (wall clock) execution time is satisfactory. In fact the speed up factors obtained are in the range fifteen, twenty. In Table 1 t*GPU,240 = tP0+P1(CPU)+tP2(GPU) is the time needed to compute P0+P1+P2 using the hybrid CUDA implementation and t*CPU is the time needed to compute P0+P1+P2 using the CPU.
The CUDA implementation of Application 1 can be downloaded here:
Application 2: Realized variance options
A European realized variance option is an option whose payoff depends on the time to maturity and on the realized variance of the log-returns of the price of the asset underlying the option in a preassigned sequence of time values ti, i = 0,1,╝,N, belonging to the time interval defined by the time when the option is priced and the maturity time of the option.
The method used to approximate the price of this option is based on the use of the Heston stochastic volatility model as model of the dynamics of the log-return of the underlying asset price and on the approximation of the discrete sum that gives the realized variance with a stochastic variable obtained integrating the stochastic variance of the Heston model on a suitable time interval that is known as integrated (stochastic) variance at the option maturity time (see [1], [2], [4] and the website http://www.econ.univpm.it/recchioni/finance/w4).
Application 2 consists in the numerical evaluation of the integral that approximates the price of the realized variance option with the price of an integrated variance option using an algorithm well suited for GPU computing (see [1]). Let m be a positive integer the problem of pricing realized variance options is reduced to the computation of a simple expression and of a one dimensional integral that is approximated using m quadrature nodes. The numerical quadrature that evaluates the integral is carried out in parallel.
In Application 2 all the functions used in the computation have been implemented using the "inline" compiler directives thanks to the use of a specific CUDA library written by one of us (M.G.) to evaluate the elementary complex functions needed to price realized variance options. A test problem consisting in pricing a realized variance option considered in [1], [2] is studied. The results obtained are presented in Tables 2 and 3. Tables 2 and 3 show the GPU speed up factors obtained using the variance option CUDA subroutine in single and in double precision. In particular Tables 2 and 3 show that running the CUDA implementation of Application 2 on the GPU in single precision the (wall clock) execution time reduces approximately of a factor 1.5 compared with the time required to run the same computation on the GPU in double precision. This fact gives a quantitative measure of the cost of transferring information on the GPU registers. Finally going from m=2562 to m=20482 the GPU speed up factor increases approximately of a factor 1.9 in Table 3 (double precision) going from 65.81 to 124.52 and of a factor 3.3 in Table 3 (single precision) going from 70.03 to 230.86. These are very impressive speed up factors.
m
tGPU,240 (sec/1000) tCPU (sec/1000) Speed up factor tCPU/tGPU,240
2562 4.27 281 65.81
5122 11.16 1141 102.24
10242 38.05 4578 120.31
20482 147.56 18375 124.52
m
2562
tGPU,240 (sec/1000) tCPU (sec/1000) Speed up factor tCPU/tGPU,240
3.57 250 70.03
5122 7.01 1046 149.22
10242 19.49 4110 210.76
20482 71.2 16437 230.86
The CUDA implementation of Application 2 can be downloaded here: