A trading execution model based on mean field games and optimal control

Lorella Fatone, Francesca Mariani, Maria Cristina Recchioni, Francesco Zirilli

In [2] we present a trading execution model that describes the behaviour of a big trader and of a multitude of retail traders operating on the shares of a risky asset. The retail traders are modeled as a population of  “conservative'” investors that: i)  behave in a similar way, ii) try to avoid abrupt changes in their trading strategies, iii) want to limit the risk due to the fact of having open positions on the asset shares, iv) in the long run want to have a given position on the asset shares. The big trader wants to maximize the revenue resulting from the action of buying or selling a (large) block of asset shares in a given time interval. The behaviour of the retail traders and of the big trader is modeled using respectively a mean field game model and an optimal control problem. These models are coupled by the asset share price dynamic equation. In particular this equation describes how the asset shares price depends from the trading activity of the retail traders and of the big trader. The trading execution strategy adopted by the retail traders is obtained solving the mean field game model. The knowledge of this strategy is necessary to formulate the optimal control problem that determines the strategy adopted by the big trader. The mathematical models considered are solved using the dynamic programming principle. Under some hypotheses the solution of the mean field game model is reduced to the solution of a (constrained) two point boundary value problem for a system of six Riccati ordinary differential equations. The optimal control problem associated to the big trader is a linear quadratic control problem. Under some hypotheses an explicit formula for the optimal trading execution strategy of the big trader is deduced. A numerical study of the trading execution model proposed is presented. The trading execution strategies obtained with the model developed in [2] and those obtained using alternative models are compared. This comparison confirms the quality of the model presented. A general reference to the work of the authors and of their coauthors in mathematical finance is the website: http://www.econ.univpm.it/recchioni/finance.

Keywords: mean field game; optimal control; trading execution strategy.

 

Content

1.      The model

2.      The solution 

3.      Numerical experiments (animation 1, animation 2, animation 3, interactive application, app)

4.      References

 

1.The model

In [2] we consider a market where a big trader and a multitude of  retail traders operate on the shares of a risky asset.

The big trader want to maximize the expected (total) revenue resulting from the action of selling a (large) number of shares of the risky asset in a given time interval (liquidation problem). The analysis developed to study the liquidation problem can be easily extended to the study of the problem posed by the execution of a buying order.

The retail traders are conservative investors that belong to a population of individuals that:

·         behave in a similar way,

·         try to avoid abrupt changes in their trading strategies,

·         want to limit the risk due to the fact of having open positions on the asset shares,

·         in the long run want to have a given position on the asset shares.

The behaviour of the big trader is modeled using an optimal control problem.

The behaviour of the retail traders is modeled using a mean field game model [4]. This means that the behaviour of the retail traders is studied in the “mean field approximation”. The (time) dynamics of the trading positions of  the retail traders is substituted with a “mean dynamics” that describes the behaviour of the trading position of a “mean retail trader”. We recall that the mean field approximation has been introduced in statistical mechanics to study systems of interacting particles and that has been used in the social sciences to describe multitudes of  “intelligent agents”.

The mathematical models that describe the big trader and the retail traders are coupled through the asset price dynamic equation.

The retail traders model

 

Let:

·         R be the set of real numbers,

·         T1ÎR be a positive number that represents the time horizon of the mean field game model that describes the retail traders. This means that  the model that describes the retail traders is solved in the time interval  [0,T1],

·         xt, tÎ[0,T1], be a real stochastic process that represents the number of shares of the risky asset held by the retail traders as a function of the time t, tÎ[0,T1]. The variable  xt is called trading execution strategy or trading position of the retail traders at time t, tÎ[0,T1]. Recall that the variable xt,  tÎ[0,T1],  describes the retail traders in the mean field approximation. Positive values of xt,  tÎ[0,T1],  mean that the retail traders have a long position on the asset shares, negative values of xt,  tÎ[0,T1],  mean that the retail traders have a short position on the asset shares,

·          be a continuous function that represents the trading rate of the retail traders,

·         m(t,x), xÎR, tÎ[0,T1], be the probability density function of the random variable xt, tÎ[0,T1],

·         σ be a (non zero) real constant,

·         Wt, , be a standard Wiener process such that W0=0 and dWt, , be its stochastic differential.

 

We assume that the trading execution strategy of the retail traders xt, tÎ[0,T1],  is solution of the following stochastic differential equation:

 

                                                                                                                                                                      (1)
                    

 

with initial condition:

                                                                                                                                                                                                                      (2)
                                                                                                                                                                                                                                                                 

where  is a known random variable whose probability density function is denoted with m0(x), xÎR. The probability density function of xt is denoted by m(t,x), xÎR, tÎ[0,T1].

Equation (1) is the mean field equation that describes the “mean dynamics” of the trading position of the “mean retail trader”.

 

Note that in (1) the function  is not a known coefficient. The function  is the control variable that must be determined solving the mean field game model.

 

Let E( denote the expected value of    ,  A1  be the set of the square integrable processes on [0,T1] , and λ, θ, a be parameters such that λ>0, θ≥0 and aÎR.

 

The retail traders adopt the trading execution strategy whose rate =t=(t,xt), tÎ[0,T1],  solves the following problem:

 

                                                                                                                                                                       (3)

where:

 

                                                                                   (4)

 

subject to the constraints (1), (2).

The model (3), (4), (1), (2) is the mean field game model used to describe the behaviour of the retail traders.

 

 

 

The big trader model and the asset share price dynamic equation

 

Let:

·         T2ÎR be a positive number such that T2≤T1,  T2 is the time horizon of the liquidation problem. This means that the selling order must be executed in the time interval [0,T2],

·         Y>0 be a positive integer that represents the number of asset shares that must be sold in the time interval [0,T2],

·         β:[0,T2] × R → R be a continuous function that represents the trading rate of the big trader,

·         yt, tÎ[0,T2], be a real function that represents the number of asset shares of the risky asset held by the big trader as a function of the time t, tÎ[0,T2]. The variable yt, tÎ[0,T2], is called trading execution strategy of the big trader.

 

The liquidation problem of the big trader consists in determining how to execute the order of selling Y asset shares in the time interval [0,T2] in order to maximize the expected (total) revenue resulting from the sale.

We assume that yt,  tÎ[0,T2], is solution of the following differential equation:

 

                                                                                                                                                                          (5)

 

with initial condition:

                                                                                                 = Y,                                                                                                                             (6)

and final condition:

                                                                                                                                                                                                                           (7)

 

The function βt= β(t,yt), tÎ[0,T2], is the control variable of the control problem that defines the behaviour of the big trader.

 

Note that the differential equation (5) is the equation used in similar circumstances by Almgren [1].

 

The asset price dynamic equation of the model presented in [2] is a simple generalization of the asset share price dynamic equation used by Almgren in [1].

 

Let:

·           be a stochastic process that represents the price of the asset share “in absence of trading”, we assume that  d= εdBt, [0,T2],  where ε>0 is a real parameter and Bt, [0,T2], is a standard Wiener process, such that B0=0 and dBt is its stochastic differential. The Wiener processes Wt, Zt and Bt, [0,T2],  are assumed to be independent.

·           ζ2 be nonnegative constants.

 

Let St be the asset share price at time t,  [0,T2], we assume that St,  [0,T2], is a real stochastic process defined as follows:

 

                                                                                          St =  + Mt + βt + ζ2(Y-yt),        tÎ[0,T2],                                                                    (8)

 

                                                                                           given,                                                                                                                               (9)

 

where Mt = E(α(t,xt)) = E(αt) = ,  t[0,T1], βt = β(t,yt), t[0,T1],  and we assume that  is a positive random variable concentrated in a point.

Equation (9) is the asset price dynamics equation.

Note that the asset price dynamic equation (9) allows negative asset share prices. The same is true for the asset share price dynamic equation used by Almgren in [1].

 

Let A2  be the set of the square integrable processes on [0,T2]. The problem of finding the optimal trading execution strategy for the big trader consists in solving the following optimal control problem:

 

                                                                                                                                                                                                               (10)

where:   

 

                                                                             V(β) = ,    βA2,                                                                                                   (11)

 

subject to the constraints  (5), (6), (7).

The problem (10), (11), (5), (6), (7), (8), (9) is a linear quadratic optimal control problem.  The function V(β), βA2 is the expected final revenue resulting from the liquidation order when the trading execution strategy yt,  tÎ[0,T2], determined by β through (5), (6), (7) is adopted.

 

 

2.The solution of the model    

Let N(∙,+) be the normal probability distribution of mean ∙ and standard deviation + and let ξ be  a random variable. The notation ξ N(∙,+) means that ξ is a normal random variable distributed  N(∙,+). Using the ideas of Kalman [3] under some hypotheses we reduce the solution of the mean field game model (3), (4), (1), (2) and of the optimal control problem (10), (11), (5), (6), (7), (8), (9) to the solution of two systems of Riccati ordinary differential equations (see [2] for more details).

 

In particular in [2] under the hypotheses that: there exist μ0, ψ0,  ψ0>0, such that   N(μ0, ψ0) we show that  N(μt, ψt),  tÎ[0,T1], where , tÎ[0,T1], is the solution of the mean field game model (4), (3), (2), (1) and μt, ψt, tÎ[0,T1], are determined from the solution of a system of six Riccati ordinary differential equations.

Moreover in [2] when  tÎ[0,T1], we derive explicit formulae for Mt, μt, t[0,T1], these formulae are substituted in the asset share price dynamic equation (8) in order to solve the optimal control problem (10), (11), (5), (6), (7), (8), (9). In [2] we show that the corresponding optimal trading execution strategy of the big trader yt= , tÎ[0,T2], solution of the problem (10), (11), (5), (6), (7), (8), (9) is the solution of the following differential equation:

                                                                                                                              (12)

with initial condition:

                                                                                                                                                                                                                          (13)

Recall that since the formulae for Mt, μt, tÎ[0,T2], deduced in [2] have been obtained under the assumption  N(μ0, ψ0) also the formula for  t[0,T2], deduced in [2] from (12), (13) holds under the assumption  N(μ0, ψ0).

 

3. Numerical experiments

Let us study the trading execution model presented in Sections 1 and 2 via numerical simulation. In particular we consider a liquidation order and in a test case we compare the value of the expected total revenue of the big trader (11) associated to the optimal trading execution strategy (12), (13) that we have found as solution of our model with the expected total revenue of two alternative trading execution strategies.

 

We assume that:

·         the number of asset shares held by the big trader at time t=0 is Y=2,

·         the final time within which the sale must be completed is T2=0.6,

·         the remaining parameters of the models of Section 1 and 2 have the following values: T1=1, =10, =1, ζ2=0, λ=0.5, σ=0.8, μ0=10, ψ0=0.5 and a=-50, θ=1.

 

Note that the choice:

·         μ0=10 implies that the retail traders are buyers at time t=0,

·         a=-50 implies that the retail traders are sellers at time T1.

 

With the previous choices the optimal trading execution strategy of the big trader determined by our model from being a concave function of t when t is close to zero becomes a convex function of t when t is close to T2.

 

To fix the ideas we consider three trading execution strategies (Strategy 1, Strategy 2, Strategy 3) that are shown in the three animations that follow.

1.      In animation 1 we show the optimal trading execution strategy of the big trader yt=, tÎ[0,T2], obtained as solution of the model presented in Sections 1 and 2 defined by (12), (13) and in [2]. This is Strategy 1.

2.      In animation 2 we show the trading execution strategy of the big trader defined as follows:

 

                                                                                                                                                              (14)

 

      where , tÎ[0,T2], is the optimal trading execution strategy shown in animation 1. This is Strategy 2.

3.      In animation 3 we show the optimal trading execution strategy of the big trader found in the “same circumstances” using Almgren’s model [1] that consists in selling with constant rate in the time interval [0,T2], that is:

 

                                                                                                                                                                                  (15)

      This is Strategy 3.

 

 

Animation 1

 

Animation 2

 

Animation 3

 

Note that Strategy 1 (see animation 1) makes use of  short selling (i.e.: yt becomes negative for some values of  tÎ[0,T2]). Strategy 2 and Strategy 3 do not use short selling.

 

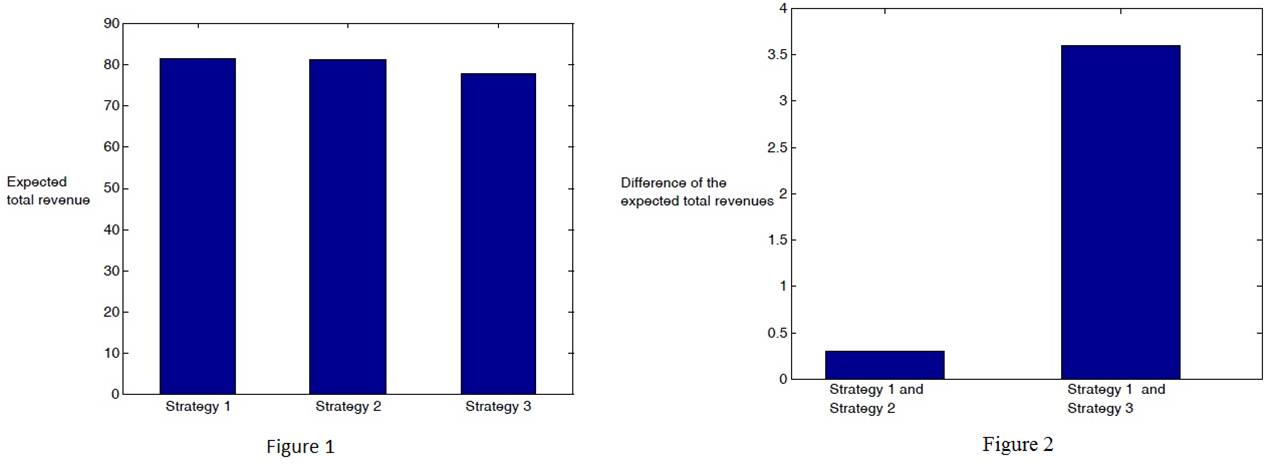
In Figure 1 we compare the values of the expected total revenue (11) associated to the trading execution Strategies 1, 2, 3. As it should be the expected total revenue associated to the optimal trading execution strategy, Strategy 1, is greater than the expected total revenues associated to Strategy 2 and Strategy 3.

 

In Figure 2 we show the difference between the expected total revenues associated to Strategy 1 and Strategy 2 and the difference between the expected total revenues associated to Strategy 1 and Strategy 3.

 

 

 

 

 

Finally an interactive application and an app are presented. The interactive application computes and draws on a graph the optimal trading execution strategy of the big trader, the mean value of the trading execution strategy of the retail traders and the asset price dynamics. In the interactive application the user must assign the values of some of the model parameters. To facilitate the use of the interactive application a set of default values of these parameters is given. The remaining parameters of the models involved in the numerical simulation are chosen as follows: =10, =1, ζ2=0, λ=0.5, σ=0.8, ψ0=0.5 and θ=1. Recall that the random variable  that appears in (9) is chosen to be a random variable concentrated in the point  (assigned by the user) with probability one.

Interactive application

 

The interactive application has been transformed in an app. The app runs on devices based on the Android software system including smart phones and tablets.

App

 

4. References

[1]  R. Almgren (2003). Optimal execution with nonlinear impact functions and trading enhanced risk. Applied Mathematical Finance 10(1), 1-18.

[2]  L. Fatone, F. Mariani, M.C. Recchioni, F. Zirilli (2014). A trading execution model based on mean field games and optimal control. Applied Mathematics 5(19), 3091-3116. 

[3]  R. E. Kalman (1960). A new approach to linear filtering and prediction problems. Journal of Basic Engineering 82 (1), 35-45.

[4]  J. M. Lasry, P. L. Lions (2007). Mean field games. Japanese Journal of Mathematics 2(1), 239-260.

[5]  D. Revuz, M. Yor (1999). Continuous Martingales and Brownian Motion. Springer-Verlag, New York.

 

 

 

Entry n.

 1