Pricing realized variance options using integrated stochastic variance options in the Heston stochastic volatility model
Lorella Fatone, Francesca Mariani, Maria Cristina Recchioni, Francesco Zirilli
The numerical experience reported here has been obtained using the computing grid of ENEA (Roma, Italy). The support and sponsorship of ENEA is gratefully acknowledged.
Warning: If your browser does not allow you to see the content of this website click here to download a postscript file that reproduces the material contained here.
This website presents a numerical method to price European options on realized variance. An European realized variance option is an option whose payoff depends on the time of maturity, on the variance of the log-returns of the stock price observed in a preassigned sequence of time values ti, i = 0,1,¼,N. That is the realized variance is the variance observed in the sample of the log-returns, so that the value at maturity of the realized variance option depends on the discrete sample of the log-returns of the stock prices observed at the times ti, i = 0,1,¼,N. The method proposed to approximate the price of these options is based on the idea of approximating the discrete sum that gives the realized variance with an integral using as model of the dynamics of the log-return of the stock price the Heston stochastic volatility model. In this way the price of a realized variance option is approximated with the price of an integrated stochastic variance option whose payoff depends on the time of maturity and on the integrated stochastic variance. The integrated stochastic variance option is priced with the method of discounted expectations. We derive an integral representation formula for the price of this last kind of options. This integral formula reduces to an one dimensional Fourier integral in the case of the most commonly traded options that have a simple payoff function. The method proposed has been validated on some test problems. The numerical experiments show that the approach suggested here gives satisfactory approximations of the prices of realized variance options (relative error 10-2, 10-3) and allows substantial savings of computational time when compared with the Monte Carlo method used to evaluate realized variance options in the Heston stochastic volatility model with approximately the same accuracy. This website contains auxiliary material that helps the understanding of the paper [1] and makes available to the interested users the (FORTRAN) codes that implement the numerical method proposed here to price realized variance options. The use of one of these codes on a computing grid has been made user friendly developing a dedicated application using the software Symphony (that is a Service Oriented Architecture (SOAM) software of Platform Computing Toronto, Canada). This website makes available to the users this Symphony application.
A detailed exposition of the material summarized in this website can be found in [1].
Realized variance and volatility derivatives are becoming increasingly important in the financial markets. To fix the ideas let Sn, n = 0,1,2,¼, N be a time series of consecutive prices of an asset, such as, for example, the daily closing value of a market index, observed at time tn, n = 0 (today),1,2,¼,N (maturity). For n = 1,2,¼,N holding a unity of the asset between time tn-1 and time tn corresponds to a return rn = ln(Sn/Sn-1). The investors are interested in the realized variance or in the realized volatility (standard deviation) of the returns. The realized variance is computed as follows:
![]()
![]()
Note that in the previous formulae we consider daily prices and the time unit is one day. That is in (1) s2 is expressed in the unit (day)-1. If the monitoring dates ti, i = 0,1,¼,N are equally spaced with step-size dt > 0, ti-ti-1 = dt, i = 1,2,¼,N, formula (1) must be modified dividing the right hand side by dt. With the choices made in (1) (daily prices, time unit one day) we have d t = 1. Derivatives on the realized variance s2 or on the realized volatility s of market indices, exchange rates between currencies are commonly traded in the financial markets where is common to consider relatively long time periods such as for example one year corresponding to approximately 252 daily closing prices (i.e. N = 251). In fact there are approximately 252 working days in a year. It is clear that these derivatives must be considered as discretely sampled path dependent options and that the samples of real interest are quite large (i.e., for example, there are 252 sample times ti in the previous example). Moreover we observe that the stochastic volatility models that describe the dynamics of the underlying asset are the natural setting to price derivatives on (realized) variance or volatility. The increasing relevance of pricing options on realized variance or other derivatives such as realized variance swaps is due to the fact that they are largely used as a vehicle for trading volatility and generates the problem of developing mathematical models to price these kinds of options and derivatives that could be solved in a computationally convenient way.
Several papers deal with this problem and the main assumptions common to these papers are frictionless markets, continuous price paths, continuous trading in the asset and a continuous of option strikes while very controversial is the need of assumptions on the volatility dynamics. Recently several authors have attempted to study realized variance options without requiring to specify the volatility dynamics but the main research papers on the subject are based on some assumptions on the dynamics of asset prices and of their volatility (see [2]-[8]).
In [1] the authors specify the volatility dynamics that is they consider the Heston stochastic volatility model to describe the dynamics of the asset prices and of their stochastic variance and they approximate the price of realized variance options with the price of integrated stochastic variance options in the context of the Heston stochastic volatility model. The Heston stochastic volatility model [5] is given by the following system of stochastic differential equations:
| (3) |
| (4) |
| (5) |
| (6) |
where S(t), t > 0, is the price of the underlying asset at time t, v(t), t > 0, is the stochastic variance of the underlying asset price at time t, w, c, q, e are constants, W1(t), W2(t), t > 0, are standard Wiener processes such that W1(0) = 0, W2(0) = 0, dW1(t), dW2(t), t > 0, are their stochastic differentials and we have:
| (7) |
where corr(·,·) is the correlation coefficient of the random variables · and · and r is a constant such that |r| < 1.
Note that in (5), (6) S0, v0 represent random variables concentrated with probability one in the real numbers S0 > 0, v0 > 0. We assume c> 0, q>0, e≥ 0. Moreover when e> 0 we assume 2cq/e2-1 > 0, this last condition guarantees that if v0 is positive v(t) remains positive (with probability one) for t > 0.
In order to consider integrated (stochastic) variance options we introduce a new equation, that is:
| (8) |
| (9) |
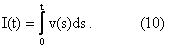
We consider the three factor model given by (3), (4), (8) where the factors are S, v, I with the initial conditions (5), (6), (9). This three factor model can be rewritten using the centered log-returns x(t), t>0, of the asset price S(t), t > 0, as follows:
| |||||||||||||||||||||||||||||
| |||||||||||||||||||||||
where x(t) = ln(S(t)/S0)-w t, t > 0. In fact it is easy to see that problem (11), (12), (13), (14), (15), (16) is equivalent to problem (3), (4), (8), (5), (6), (9).
Using the risk neutral formula in order to evaluate at time t=0 an integrated (stochastic) variance option with maturity T > 0 and payoff function P(I) (for example P(I) = max{I-E,0} where E is a strike variance) we must evaluate:
![]()
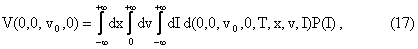
where d(0,0,v0,0,T,x,v,I) is the appropriate transition probability density associated to (11), (12), (13) with the initial conditions (14), (15), (16) (see Section 3).
The quantity V(0,0,v0,0) can be multiplied by a discount factor to take care of a nonzero constant risk free interest rate. In the following for simplicity we assume that this discount factor is equal to one. We call the stochastic variance options whose payoff function P(I) is a function only of I integrated stochastic variance options. The integral (17) is a three dimensional integral that can be computed numerically using elementary quadrature rules when the transition probability density d(0,0,v0,0,t,x,v,I) is known on a suitable grid. However due to the special character of the Heston model and to the special character of the three factor model (11), (12), (13) considered here ad hoc numerical methods can be developed to evaluate (17). The numerical method developed here to evaluate d(0,0,v0,0,t,x,v,I) and V(0,0,v0,0) is based on the integral representation formula that gives the fundamental solution of the Fokker Plank equation relative to (11), (12), (13), and, when no assumptions are made on the explicit form of the function P(I), on the evaluation of the integrals necessary to price the integrated stochastic variance option using the Fast Fourier Transform (FFT). This numerical procedure is very efficient and very well suited for parallel computing. When the most common choices of P(I) are made (i.e., for example, P(I) = max{I-E,0}, where E is a strike variance) a more detailed analysis of (17) is possible. Some numerical examples on test cases obtained with a software implementation of the numerical method proposed are presented and discussed.
The reader not interested in mathematical details may jump to the numerical results of Section 3 or to Section 4.
We begin deriving a formula for the transition probability density d(t0,x0,v0,I0,t,x,v,I), 0 £ t0 < t, associated to the stochastic dynamical system (11), (12), (13) that is the probability density of having x(t)=x, v(t)=v, I(t)=I given x(t0)=x0, v(t0)=v0, I(t0)=I0. We assume v0 ³ 0, I0 ³ 0 since this is the case of practical interest. We note that d depends only on the difference t-t0 so that we define:
| (18) |
The function p(t,x0,v0,I0,x,v,I) satisfies the following initial value problem:
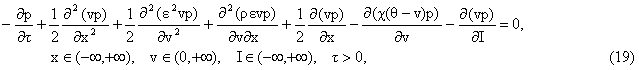
| ||||||||||||||||
Using a procedure similar to the one described in [7] p. 602-607 and the risk neutral formula, it is possible to derive the following formula for the price at time t=t0 of an integrated variance option maturing at time t=t0+t and whose payoff function P depends only on the integrated stochastic variance that is when we consider P(x,v,I) = P(I):
![]()
We note that when we consider an integrated stochastic variance option with maturity time T and we evaluate the contract at t=t0 = 0 we have S(0) = S0, I(0) =I0 = 0, x(0) = x0 =ln(S(0)/S0)-w0 = 0, t=T. Remind that options with payoff function depending only on I are called options on the integrated stochastic variance.
Finally with the choices made in formula (21) when the payoff P(I) is given by P(I) = max{I-E,0} for some positive constant E we can express the corresponding option value, Vs, as follows:
![]()
where we remind that t=t0+t is the time of maturity of the option and the function s(x,E) of the real variable x is given by:
![]()
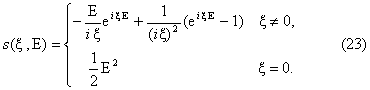
Note that formula (22) is derived from formula (21) with simple manipulations and consists of a one dimensional integral of an explicitly known integrand. The numerical evaluation of formula (22) is an elementary problem that can be solved by numerical quadrature. Formulae analogous to (22) can be derived when the payoff function P(I) = max {I-E,0 } is substituted with any other "reasonable" expression.
We compare the results obtained with the method described above when the payoff function is given by P(I) = max {I-E,0 } with the numerical results obtained integrating numerically the stochastic dynamical system (11), (12) equipped with the initial condition (14), (15) to get H samples of the log-returns xij = x(ti), i = 1,2,¼,N, j = 1,2,¼,H where ti-ti-1 = T/N, i = 1,2,¼,N and we compute the price of the realized variance option first computing H samples of the realized variance:
![]()
![]()
and then taking the following average:
![]()
It is easy to see how to change formula (26) when we consider a generic payoff function instead than the special choice P(I)=max{I-E,0} considered in (26)
We consider two numerical experiments. The parameters of the first experiment (see [5]) are chosen as follows:
| (27) |
With this choice we have 2cq/e2-1 = 3. In Table 1 we show the prices VI of the options obtained with a numerical implementation of formula (22) when t0=0, x0=0, I0=0, t=T using the numerical technique proposed in [9] and the prices V252 obtained with the Monte Carlo simulation described above when we have N = 252 monitoring dates for two choices of the variance strike price E and three choices of v(0) = v0. We always choose the time unit to be one year, and the maturity time of the option T = 1 year so that the time step dt is equal to 1/N and, as done in formula (24) when T=1, we need to divide formula (1) by dt. Table 1 shows from left to right T, E, v0, V252, VI. The last four columns show the relative error er = |VI-V252|/|V252|, the ratio Rt = tMC/tI where tMC and tI are the execution times measured using the Fortran function secnds of the program implementing the Monte Carlo method (tMC) and of the program that computes VI using formula (22) (tI), the relative standard deviation sN of the result obtained in the Monte Carlo simulation and the absolute value Ip of the imaginary part of VI. Note that the imaginary part of Vs is zero so that the imaginary part of VI gives a measure of the accuracy of the numerical integration. The Monte Carlo integration has been carried out using a sample of H = 2·107 realizations of the payoff function.
We remind that when the quantity 2cq/e2-1 is small and positive the numerical integration of the stochastic dynamical system (11), (12) is a delicate problem since the numerical integration may fail to find v(t), t > 0, positive even if we start from a positive value of v(0).
| T | E | v0 | V252 | VI | er | Rt | sN | Ip |
| 1 | 0.05 | 0.2 | 4.183e-02 | 4.214e-02 | 7.411e-03 | 15122.46 | 7.583e-05 | 1.124e-09 |
| 1 | 0.05 | 0.4 | 1.280e-01 | 1.286e-01 | 4.687e-03 | 14460.02 | 4.115e-05 | 3.872e-12 |
| 1 | 0.05 | 0.8 | 3.002e-01 | 3.015e-01 | 4.330e-03 | 14287.30 | 3.099e-05 | 2.039e-16 |
|
1 | 0.1 | 0.2 | 2.630e-03 | 1.537e-03 | 4.155e-01 | 15217.86 | 5.234e-04 | 2.094e-09 |
| 1 | 0.1 | 0.4 | 7.792e-02 | 7.861e-02 | 8.855e-03 | 14930.16 | 6.754e-05 | 8.411e-12 |
| 1 | 0.1 | 0.8 | 2.502e-01 | 2.515e-01 | 5.194e-03 | 14158.32 | 3.719e-05 | 3.998e-16 |
| T | E | v0 | V252 | VI | er | Rt | sN | Ip |
| 1 | 0.5 | 0.8 | 9.522e-02 | 9.338e-02 | 1.932e-02 | 3895.63 | 1.891e-04 | 2.660e-04 |
| 1 | 0.5 | 1.5 | 5.708e-01 | 5.714e-01 | 1.051e-03 | 3738.90 | 1.714e-04 | 6.430e-06 |
| 1 | 0.5 | 2.0 | 9.149e-01 | 9.156e-01 | 7.651e-04 | 4372.81 | 4.198e-05 | 1.235e-06 |
The second experiment is analogous to the first one but we compute VI using formula (21). The results obtained in the second experiment are shown in Table 2. The parameters of the second experiments are chosen as follows:
| (28) |
We note that in Table 1 and Table 2 the agreement between V252 and VI deteriorates when v0 decreases. This is due to the fact that in the differential equations (11), (12) the v1/2 term is not Lipschitz continuous in v=0. The time step used in the numerical integration of (11), (12) must decrease when v decreases. The results contained in the V252 column are obtained using Euler method with a constant time step and deteriorate when v0 decreases. That is when v0 is small we expect the results of the VI column to be of greater quality than the results of the V252 column.
The archive UnivPM_IVOP.zip contains the following files:
one_dim.for: a Fortran main code that computes
the price of an integrated stochastic variance option
when the payoff is given by P(I)=max{I-E,0}. The input output parameters are explaind in the Fortran codes.
two_dim.for: a Fortran code that computes
the price of an integrated stochastic variance option
when the payoff function is a function supplied by the user.
The input output parameters are the same than those of the Fortran code one_dim.for.
IVOP_Symph evaluates at t=t0=0 the price of a realized variance option with maturity time t=T and payoff function P(I)=max{I-E,0} where E is the strike variance.
The use of the numerical method proposed here when P(I)=max{I-E,0} has been implemented leveraging the Symphony software from Platform Computing http://en.wikipedia.org/wiki/Service-oriented_architecture or http://www.service-architecture.com/web-services/articles/service-oriented_architecture_soa_definition.html. Symphony can be used to address the parallelization and distribution of mission critical risk and pricing calculations on a grid in near real time to deliver improved performance. Built on Platform EGO, Symphony provides a simple interface to build, test and grid-enable and manage the application service that performed the calculation of the integrals derived previously (i.e.: one_dim.for) to approximate the price of a realized variance option. The use of grid computing middleware such as Symphony allowed us to focus on the core mathematical algorithm rather than systems middleware. The forum area is here: http://www.hpccommunity.org/f6/
The IVOP_Symph application makes available in the Symphony environment the program one_dim.for.
We invite the user to fill up the following
request of informations. We plan to use the informations acquired in this
way for the
following purposes:
1) improving the quality of this website and of the
software codes UnivPM_IVOP and IVOP_Symph,
2) enlarging our knowledge of mathematical finance through
the knowledge and understanding of
the problems of interest to the users of this website.
|
|