PAPER:
An explicitly
solvable multi-scale stochastic volatility
model: option pricing and calibration problems *
Lorella Fatone, Francesca Mariani, Maria Cristina Recchioni, Francesco Zirilli
- Abstract
- Introduction
- Calibration
problem using synthetic data (movies)
- Calibration
problem and forecasting experiments using real data (movies)
- References
Warning: If your browser does not allow you to see the content of this website click
here to download a
word file that reproduces the material contained here.
In [3] we study an explicitly solvable multiscale stochastic
volatility model that generalizes the Heston model. The model describes the
dynamics of an asset price and of its two stochastic variances using a system
of three Ito stochastic differential equations. The two stochastic variances
vary on two different time scales and can be regarded as auxiliary variables
introduced to model the dynamics of the asset price. Under some assumptions the
transition probability density function of the stochastic process solution of
the model is represented as a one dimensional integral of an explicitly known
integrand. In this sense the model is explicitly solvable. In mathematical
finance multiscale stochastic volatility models are used for several purposes
such as, for example: i) the study of commodity prices, in fact usually
commodity prices are characterized by spikes that can be modeled using a fast
time scale volatility together with a standard time scale volatility, ii) the
study of financial products that live for long time periods (such as life
insurance contracts) that can be modeled using a long time scale volatility
together with a standard time scale volatility. In alternative to multiscale
stochastic volatility models the stochastic jump models, such as, for example,
Lévy's processes with stochastic volatility, can be used. However this last
type of models is explicitly solvable only in very special circumstances and in
general the transition probability density functions associated to them are
defined as solutions of integro-differential equations that must be solved
numerically. So that the use of jump models in practical situations is, in
general, cumbersome when compared to the use of the model proposed here. In
order to use the multiscale stochastic volatility model considered to compute
option prices we define its risk neutral measure and the associated risk
premium parameters. In [3] we derive a formula for the
price of the European vanilla (call and put) options in the multiscale stochastic
volatility model. The formulae obtained are given as one dimensional integrals of explicitly
known integrands and in a special case reduce to the corresponding formulae in
the Heston model [7].
This last formula in the case of a European vanilla call option improves the
formula given in Heston [7] formula (10) in a sense made
clear later. We use the option price formulae obtained to study the values of
the model parameters, of the correlation coefficients of the Wiener processes
defining the model and of the initial stochastic variances implied by the
``observed" option prices using both synthetic and real data. The real
data analyzed are those relative to the S&P 500 index in the year 2005.
That is we generalize to the model proposed here the so called term structure
analysis of the implied volatility used in the Black Scholes model. This
analysis is translated in the solution of a constrained nonlinear optimization
problem with an objective function containing an integral that must be
evaluated numerically. The real data analysis presented shows that the
multiscale stochastic volatility model gives a satisfactory explanation of the
observed option prices including those of the out of the money options and that
the implied values of the model parameters, of the correlation coefficients and
of the initial stochastic variances can be used to obtain high quality
forecasts of the option prices. This website contains some auxiliary material
including some animations that helps the understanding of [3].
A more general reference to the work of the authors and of their coauthors in
mathematical finance is the website: http://www.econ.univpm.it/recchioni/finance.
We
present a multiscale stochastic volatility model in mathematical finance.
Multiscale modeling is used in a variety of scientific and technical fields and
there are many problems that can be described satisfactorily within a multiscale
framework (such as, for example, problems in turbulent flow, porous media,
weather forecasting, material science, wave propagation, microstructure
simulation and biological cell behaviour). However only recently multiscale
models have attracted the attention of the mathematical finance community. In [3] we consider the use of multiscale models in the study of
the stochastic volatility associated to an asset price. The idea of using
stochastic volatility models to describe the dynamics of an asset price derives
from the empirical evidence that the asset price dynamics is driven by
processes with non constant volatility. In fact when the constant volatility
Black and Scholes model [1] is used to interpret financial
data two phenomena are observed: (i) the volatility “smile” that appears in the
volatilities implied by the observed option prices, (ii) the presence of
skewness and kurtosis in the asset price probability density function deduced
from the empirical data. These phenomena show that the Black Scholes model
fails to describe correctly the market behaviour. Several alternatives have
been proposed to improve the market description, among them we consider
specifically the stochastic volatility models. In these models the stochastic
volatility or the stochastic variance of the asset price is defined as the
solution of a stochastic differential equation that is coupled with the asset
price stochastic differential equation. Models of this type are, for example,
the Heston model [7], that has received special attention
since in several circumstances it is able to describe satisfactorily the price
dynamics of relevant assets. Furthermore the Heston stochastic volatility model
is an explicitly solvable model in the sense that in the Heston model the joint
probability density function associated to the asset price and to its
stochastic variance can be written as a one dimensional integral of an
explicitly known integrand. Heston in [7] derived a formula
for the price of a European vanilla call option in the Heston model given by a
one dimensional integral. Later Lipton [8] pagg. 602-605
derived for the Heston model a representation formula for the joint probability
density function of the asset price and of the associated stochastic variance
given by a one dimensional oscillatory integral of an explicitly known
integrand and he used this formula to price forward starting options. Using the
ideas presented in [8]
pagg. 602-605 we have derived in [4], in the Heston
model framework, an integral representation formula for the prices of European
vanilla options that involves only a one dimensional integral of an explicitly
known integrand. In a sense explained in [3] and
summarized here at the end of this Section the formulae derived in [9] and refined in [4], are different from that derived in [7] and are an improvement
of the formula derived in [7].
In
the construction of the multiscale stochastic volatility model proposed we
start from the fact that several empirical studies of real data have shown that
the term structure of the implied volatility of the price of several
underlyings (such as, for example, market indices, commodities,....) seems to
be driven by two different factors: one fluctuating on a fast time scale and
the other fluctuating on a long time scale. Moreover it has been observed that the
financial derivatives with long residual life are not priced satisfactorily by
one factor stochastic volatility models such as the Heston model. That is there
is empirical evidence of the fact that in the circumstances mentioned above one
factor stochastic volatility models are inadequate to fully capture the
volatility smile and the volatility dynamics. In the last two decades several
authors have developed models able to deal satisfactorily with at least one of
the market features mentioned previously. In particular for this purpose two
different classes of models have been developed, that is: the multiscale
stochastic volatility models (see for
example [6], [3]), and the jump
models (see for example [2]). Usually the first kind of
models are used to price financial derivatives having medium or long residual
life while the second kind of models are used to price derivatives with short
residual life on underlyings whose prices have spikes. In particular we mention
the jump models containing exponential Lévy processes, these models have been
widely used to describe market fluctuations and to price derivatives (see for
example [2]). In general when exponential Lévy processes
are used option prices are obtained as solutions of suitable
integro-differential equations and ad hoc numerical methods must be used to
compute them (see [2], Chapter 12). However in some one
factor Lévy process model the characteristic function of the probability
density function of the log-return of the underlying asset price can be
expressed as an elementary function and the corresponding European vanilla
option prices can be computed as a double integral having as integration
variables the log-return of the underlying asset price and its conjugate
variable in the Fourier transform.
Since
empirical studies (see [3] and the reference therein)
have shown that the volatility dynamics of the price of many important assets
is governed by two factors, a highly persistent factor and a quickly mean
reverting factor, it is natural to believe that in these circumstances
multiscale stochastic volatility models can describe satisfactorily the
volatility dynamics. For these reasons we advocate the idea of using multiscale
volatility models instead than jump models to describe the asset price
dynamics.
We
use multiscale stochastic volatility models in their simplest form, that is we
use a two scale stochastic volatility model to study medium-long time scale
phenomena and fast-medium time scale phenomena. We propose a multiscale stochastic
volatility model (i.e. a three factor stochastic volatility model) that
generalizes the Heston model and that, under some hypotheses specified later,
is explicitly solvable in the sense that it is possible to write a formula for
its transition probability density function given by a one dimensional integral
of an explicitly known integrand. Starting from this representation formula for
the transition probability density function we derive two formulae given by one
dimensional integrals of explicitly
known integrands to price European
vanilla (call and put) options on an underlying asset whose price dynamics is
described by the multiscale stochastic volatility model.
Let
us go into details. Let t be a real variable that denotes time, we consider the
(vector valued real) stochastic process (xt,v1,t, v2,t),
t > 0, solution of the following system of
stochastic differential equations:
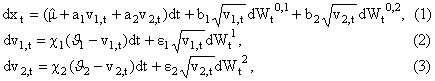
where
the asset log-return state variable xt is related with the asset price St
, t>0, via the following relation:
![]() (4)
(4)
The state variables v1,t, v2,t ,
t>0, are the stochastic variances associated to xt, t>0, Wt0,1,
Wt0,2 ,Wt1, Wt2,
t>0, are standard Wiener processes such that W00,1= W00,2=W01=W02=0, dWt0,1, dWt0,2
,dWt1, dWt2 are their
stochastic differentials and <dWt0,1dWt0,2
>= 0, <dWt0,1dWt1
>= r0,1dt, <dWt0,2dWt2
>= r0,2dt, <dWt1dWt2>=0 , where < × > denotes the mean of × and r0,1, r0,2Î[-1,1] are constants
known as correlation coefficients. The quantities ![]() ,
, ![]() , i=1,2 are real constants. The fact that the model is a two scale
stochastic volatility model is translated in the assumption that
, i=1,2 are real constants. The fact that the model is a two scale
stochastic volatility model is translated in the assumption that ![]() . The equations (1), (2), (3) must be equipped with an initial condition,
that is:
. The equations (1), (2), (3) must be equipped with an initial condition,
that is:

The random variables ![]() ,
, ![]() ,
, ![]() are assumed to be
concentrated in a point with probability one and we have
are assumed to be
concentrated in a point with probability one and we have ![]() =0. Later we will assume
=0. Later we will assume ![]()
![]() ,
, ![]() >0, i=1,2 and when we use the multiscale model we will
choose ai=-1/2, bi=1, i=1,2.
>0, i=1,2 and when we use the multiscale model we will
choose ai=-1/2, bi=1, i=1,2.
We conclude this Section noting that when we
evaluate the option prices we use the no
arbitrage pricing theory, that is we compute the option price as expected value
of a discounted payoff with respect to an equivalent martingale measure, known
as risk-neutral measure. The risk neutral measure is a probability measure
equivalent to the statistical measure associated to the process (1), (2), (3)
that guarantees that the discounted value of the underlying is a martingale.
When we assume that the volatility is constant, the risk neutral measure is
unique. In the case of one factor stochastic volatility models, such as the
Heston model, this uniqueness does not hold anymore and we have a family of
risk neutral measures parameterized by a real parameter called risk premium
parameter. It is easy to see that in the case of the multiscale stochastic
volatility model (1), (2), (3) we have a family of risk neutral measures
parameterized by two risk premium parameters l1 and l2. This family of measures is given
by the statistical measures associated to the following dynamical systems:
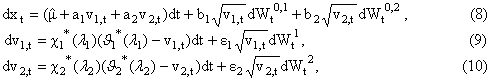
equipped with the initial conditions (5), (6),
(7), where ci*(li) = ci+li, q*i(li) = ciqi/(ci+li), i =
1,2, where ci, qi, i=1,2
are the constants appearing in the stochastic differential system (1), (2), (3)
and the real parameters li, i = 1,2 are the risk premium parameters. We
impose c*i(li) ³ 0, q*i(li) ³ 0, i =1,2, that is we impose li > -ci, i = 1,2.
In [3] we use the risk neutral measure defined through (8), (9), (10) to derive formulae involving one dimensional integrals of explicitly known integrands to price European call and put vanilla options. These formulae when we choose a1=0, a2=-1/2, b1=0, b2=1 price European vanilla options under the Heston model. The formula derived in [3] for the price of a European vanilla call option under the Heston model improves the well known formula derived in [7] to price options under the Heston model (see formula (10) of [7]). In fact the formula derived in [7] does not generalize naturally the Black Scholes formula since it is not the expected value of the discounted payoff computed using the risk neutral measure induced by the fundamental solution of the Fokker Planck equation associated to the Heston dynamical system. This is due to the fact that the measure used by Heston in [7] is not a probability density in the two variables log-return and stochastic variance at the initial time t=0 and, as a consequence, it is not a probability density function at time t, t > 0. The formula derived in [3] instead is truly analogous to the original Black Scholes formula in the context of the stochastic volatility models considered.
3. Calibration
problem using synthetic data
The
calibration problem that we solve consists in determining the values of the
model parameters, of the correlation coefficients and of the initial stochastic
variances that give the best approximation of the option prices used as data.
We consider the approximation in the least squares sense so that we reformulate
the calibration problem as a nonlinear constrained least squares problem.
In
the numerical experiments proposed here and in Section 4 we
choose in equations (1), (2), (3) a1 = a2 = -1/2
and b1 = b2 = 1. Let us denote with Q = (e1,q1,r0,1,c1,![]() ,
, ![]() ,l1,e2,q2,r0,2,c2,
,l1,e2,q2,r0,2,c2, ![]() ,l2) the vector of the parameters of the
multiscale model (including the risk premium parameters), of the correlation
coefficients and of the initial stochastic variances and let m be a positive integer,
we denote with
,l2) the vector of the parameters of the
multiscale model (including the risk premium parameters), of the correlation
coefficients and of the initial stochastic variances and let m be a positive integer,
we denote with ![]() Î R+ the price of the asset at time t, t ³ 0, with Ct(
Î R+ the price of the asset at time t, t ³ 0, with Ct(![]() ,Ti,Ki), i = 1,2,¼,m, the data, that is the prices at time t of the European vanilla call
options having maturity time Ti and strike price Ki, i =
1,2,¼,m, and with CMt,Q(
,Ti,Ki), i = 1,2,¼,m, the data, that is the prices at time t of the European vanilla call
options having maturity time Ti and strike price Ki, i =
1,2,¼,m, and with CMt,Q(![]() ,Ti,Ki), i = 1,2,¼,m, the prices of the same European vanilla call options obtained using
formula (59) of [3] that prices European vanilla call
options in the multiscale stochastic volatility model considered taking as
maturity time t = Ti-t, i = 1,2,¼,m, and as asset price S0 =
,Ti,Ki), i = 1,2,¼,m, the prices of the same European vanilla call options obtained using
formula (59) of [3] that prices European vanilla call
options in the multiscale stochastic volatility model considered taking as
maturity time t = Ti-t, i = 1,2,¼,m, and as asset price S0 = ![]() . When necessary we denote with CHt, Q(
. When necessary we denote with CHt, Q(![]() ,Ti,Ki), i = 1,2,¼,m, and with CBt, Q(
,Ti,Ki), i = 1,2,¼,m, and with CBt, Q(![]() ,Ti,Ki), i = 1,2,¼,m, the prices of the same options obtained using the Heston formula,
that is the formula deduced from the multiscale formula when we choose a1
= 0 , b1 = 0, a2 = -1/2 and b2 = 1, and the Black
Scholes formula respectively.
,Ti,Ki), i = 1,2,¼,m, the prices of the same options obtained using the Heston formula,
that is the formula deduced from the multiscale formula when we choose a1
= 0 , b1 = 0, a2 = -1/2 and b2 = 1, and the Black
Scholes formula respectively.
Note that CHt, Q and CBt, Q
depend only on some of the components of the vector Q. Please note that in the
experiments presented in this website and in [3] we use
as data only the prices of call options. More general sets of data will be considered
elsewhere.
Let R13 be the
13-dimensional real Euclidean space and let M be the set of the
admissible vectors Q, that is:
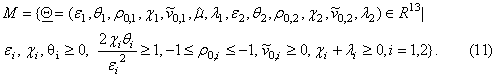
The
constraints that define M translate
some elementary properties of the model (1), (2), (3).
At time t,
t ³ 0, the calibration problem considered is
translated into the following nonlinear least squares problem:
|
(12) |
where the
objective function Lt( Q) is defined as follows:
![]()
When needed we solve problem (12) replacing CMt,Q with CHt,Q or
with CBt,Q. The formulation of the calibration
problem through (11), (12), (13) is only one formulation among many other
possible formulations. It is known that the objective function (13) may have
flat regions where the objective function changes slightly in correspondence of
significant changes of the independent variables. So that special attention
must be devoted to the choice of the initial guess of the iterative procedure
used to solve the minimization problem (12). In fact in order to choose the
initial guess of the minimization procedure we first explore the feasible
region M taking a set of (feasible) random points and evaluating the
objective function on this set of points. From these points we select a subset
of points to be used as initial guesses. We solve the optimization problem (12)
using a projected steepest descent method. This method is an iterative
procedure that, starting from an initial feasible vector Q0,
generates a sequence {Qn}, n =
0,1,¼ of feasible vectors, Qn Î M, n = 0,1,¼, moving along a descent direction obtained via a suitable projection on
the active constraints of minus the gradient with respect to Q of Lt. The optimization procedure stops when the vector Qn
generated satisfies for the first time the following criterion:
|
(14) |
where etol
and nmax are positive constants that will be chosen later.
Let
us present a numerical experiment using synthetic data (i.e.: synthetic option
prices). This experiment shows that the
formulation of the calibration problem (11), (12), (13) is able to determine
the model used to generate the synthetic option prices. We generate three sets
of synthetic data, that is three sets of synthetic option prices. The first set
is obtained generating the option prices with the Black Scholes formula choosing
the volatility s equal to ![]() and the risk free
interest rate r equal to 0.03, the second one is obtained generating the option
prices with the Heston model formula obtained using the formula derived in [4], [3] and choosing the parameters a1 =
0, b1 = 0, a2 =-0.5, b2 = 1 and
and the risk free
interest rate r equal to 0.03, the second one is obtained generating the option
prices with the Heston model formula obtained using the formula derived in [4], [3] and choosing the parameters a1 =
0, b1 = 0, a2 =-0.5, b2 = 1 and ![]() , q2 = 0.5, c2 = 9.9, r2 = -0.06, e2 = 0.4, l2 =-0.1,
, q2 = 0.5, c2 = 9.9, r2 = -0.06, e2 = 0.4, l2 =-0.1, ![]() 2,0 = 0.5. The third one is obtained generating
the option prices using the multiscale model formula contained in [3] choosing
2,0 = 0.5. The third one is obtained generating
the option prices using the multiscale model formula contained in [3] choosing ![]() , q1 = 0.8, q2 = 0.5, c1 = 1.5, c2 = 9.9, r1 = -0.04, r2 = -0.06, l1 = -0.05, l2 = -0.1, e1 = 0.4, e2 = 0.2,
, q1 = 0.8, q2 = 0.5, c1 = 1.5, c2 = 9.9, r1 = -0.04, r2 = -0.06, l1 = -0.05, l2 = -0.1, e1 = 0.4, e2 = 0.2, ![]() 1,0 = 0.8,
1,0 = 0.8, ![]() 2,0 = 0.5. In the generation of the Heston and of
the multiscale option prices we choose the risk free interest rate
2,0 = 0.5. In the generation of the Heston and of
the multiscale option prices we choose the risk free interest rate ![]() . The synthetic data generated with the Black Scholes
formula, with the Heston formula and with the multiscale formula have been perturbed with an additive
stochastic noise uniformly distributed of magnitude in absolute value at most
equal to 1% of the absolute value of the datum perturbed.
. The synthetic data generated with the Black Scholes
formula, with the Heston formula and with the multiscale formula have been perturbed with an additive
stochastic noise uniformly distributed of magnitude in absolute value at most
equal to 1% of the absolute value of the datum perturbed.
We
calibrate the multiscale model solving the constrained least squares
optimization problem (12) with the variable metric steepest descent procedure
announced previously choosing in (14) etol = 0.03 and nmax
= 10000.
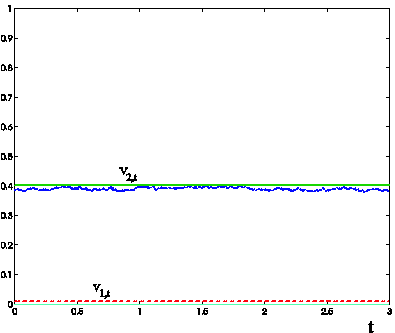
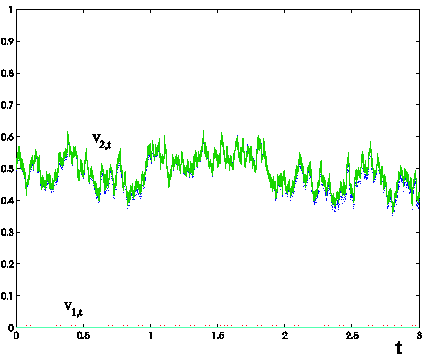
Figures
1, 2, 3 show the trajectories of the slow varying variance v1,t, t >0, and of the fast varying variance v2,t, t>0, obtained calibrating the model on the previous three sets of data and
the “true” trajectories of the stochastic variances v1,t, v2,t,
t >0, obtained integrating the Black Scholes
model, the Heston model and the multiscale model with the “true” parameters, correlation coefficients and stochastic initial variances. Note that the
“true” trajectories of the stochastic variances together with the corresponding
“true” trajectories of the asset price are the trajectories used to generate the synthetic data and that
when we use the asset price ![]() at time t>0
in (13) the quantities
at time t>0
in (13) the quantities ![]() coming from the solution of the calibration problem
(11), (12), (13) must be interpreted as
the stochastic variances at time t>0.
coming from the solution of the calibration problem
(11), (12), (13) must be interpreted as
the stochastic variances at time t>0.
Figures
1, 2 show the results obtained using as data the option prices generated by the Black Scholes and the
Heston models respectively. These Figures show that the paths reconstructed
with the calibration procedure of the stochastic variance v1,t, t > 0, are substantially constant and that the estimated values of v1,t,
t > 0, are small. While the paths obtained solving
the calibration problem using the third set of data, that is the data generated
using the multiscale model, show that the calibration procedure works correctly
(Figure 3). Furthermore in the case of the first set of data that is the data
generated using the Black Scholes model (Figure 1) the reconstructed stochastic
variance v2,t, t > 0, is substantially constant. This
is in agreement with the well known properties of the Black Scholes model.
Figure 1: Trajectories of the stochastic
variances v1,t (red dotted line corresponding to a reconstructed c1
approximately equal to 9.96·10-4), v2,t (blue dotted line
corresponding to a reconstructed c2 approximately equal to 7.71) obtained solving
the calibration problem using as data the option prices generated with the
Black Scholes model and trajectory of the ``true" Black Scholes variance
(green line) versus time t
Figure 2: Trajectories of the stochastic
variances v1,t (red dotted line corresponding to a reconstructed c1
approximately equal to 7.93·10-3), v2,t (blue dotted line
corresponding to a reconstructed c2 approximately equal to 7.68) obtained solving
the calibration problem using as data the option prices generated with the
Heston model and trajectory of the ``true" Heston variance (green line)
versus time t
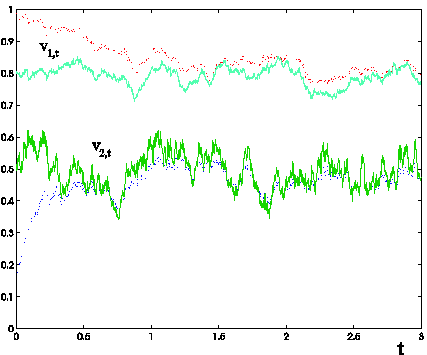
Figure 3: Trajectories of the stochastic
variances v1,t (red dotted line corresponding to a reconstructed c1
approximately equal to 8.84·10-1), v2,t (blue dotted line
corresponding to a reconstructed c2 approximately equal to 5.5) obtained solving
the calibration problem using as data the option prices generated with the
multiscale model and trajectory of the ``true" stochastic variances of the
multiscale model (green lines) versus time t
For the three models considered (Black Scholes, Heston, multiscale [3]) the following movies show a sample trajectory of the log-return xt obtained
using the vector ![]() obtained solving the
calibration problem (12) and the same sample trajectory obtained using the “true” vector
obtained solving the
calibration problem (12) and the same sample trajectory obtained using the “true” vector ![]() as function of time.
This “true” vector is the one used to
generate the data of the calibration problem.
as function of time.
This “true” vector is the one used to
generate the data of the calibration problem.
|
Black Scholes
model |
|
|
Heston model |
|
|
Multiscale model |
4. Calibration problem and forecasting experiments using real data
In
this Section we propose some experiments that use real data. We consider three models
that is the Black Scholes model, the Heston model and the multiscale model
(1),(2),(3). We study the values of the model parameters (including the risk
premium parameters), of the correlation coefficients and of the initial
stochastic variances implied by the observed prices (available to us) of the
European vanilla call options on the S&P 500 index of the New York Stock
Exchange in the year 2005 and we show that the multiscale stochastic volatility
model captures satisfactorily the ``smile" effect. To avoid excessive
numerical work we analyze the market data (i.e. S&P 500 index and the
corresponding option prices) only in the
months of January, June and November, 2005. The results presented relative to
these months are representative of the results obtainable from an exhaustive
analysis of the 2005 data. We have solved the calibration problems relative to
the Black Scholes model, to the Heston model and to the multiscale model, using
the call option prices of January 3,
2005, or of June 3, 2005 and or of November 3, 2005. The formulation of the calibration problem for
the Black and Scholes model and for the Heston model is analogous to the
formulation (11), (12), (13) used for the multiscale model. Note that for each model (Black Scholes,
Heston, multiscale) we have solved the calibration problem three times (using as
data the prices of January 3, June 3, November 3, 2005 respectively) and that
since we use all the call option prices available the calibration procedure
works simultaneously on out of money, at the money and in the money options. In
the stopping criterion (14) of the optimization procedure we use etol=0.05
and nmax = 10000. We note that in some cases the optimization
procedure stops because we have n > nmax, in these cases the
smallest value of etol reached is approximately 0.07.
Once
solved the calibration problems, we use the calibrated models to forecast the
option prices in future days using the Black Scholes formula or the Heston formula or the multiscale model formula (see [3] for the explicit form of these formulae). In these
formulae the asset price value used is the asset price value actually observed
in the day of the forecast. We forecast the stochastic variances v1,t,
v2,t, t > 0, using the mean values ![]() 1,t| Q,
1,t| Q, ![]() 2,t| Q, t > > t0, conditioned to the estimates made at time t =t0
of the random variables v1,t, v2,t, t > t0, that we denote with F0 (i.e.:F0
= (
2,t| Q, t > > t0, conditioned to the estimates made at time t =t0
of the random variables v1,t, v2,t, t > t0, that we denote with F0 (i.e.:F0
= (![]() 1,0,
1,0, ![]() 2,0)) (see [3], [4] for further details), that is using the formulae:
2,0)) (see [3], [4] for further details), that is using the formulae:

where E( · )
is the expected value of · , and ![]() , i = 1,2 are the initial stochastic variances at time t=t0
obtained solving the calibration problem. Note that in the analysis of the real
data t=t0 corresponds to January 3, or to June 3, or to November 3,
2005, and that we can translate the origin of the time axis to t0.
, i = 1,2 are the initial stochastic variances at time t=t0
obtained solving the calibration problem. Note that in the analysis of the real
data t=t0 corresponds to January 3, or to June 3, or to November 3,
2005, and that we can translate the origin of the time axis to t0.
Let
nobs be a positive integer that is the number of call option prices
at time t available in a given day, and let Ct(![]() ,Ti,Ki), CBt, Q(
,Ti,Ki), CBt, Q(![]() ,Ti,Ki), CHt, Q(
,Ti,Ki), CHt, Q(![]() ,Ti,Ki), CMt, Q(
,Ti,Ki), CMt, Q(![]() ,Ti,Ki) denote respectively the prices
of European call options with strike price Ki and maturity time Ti
(that corresponds to time to maturity ti = Ti-t) observed, generated by
Black Scholes formula, generated by Heston formula and generated by multiscale formula, i=1,2,…, nobs.
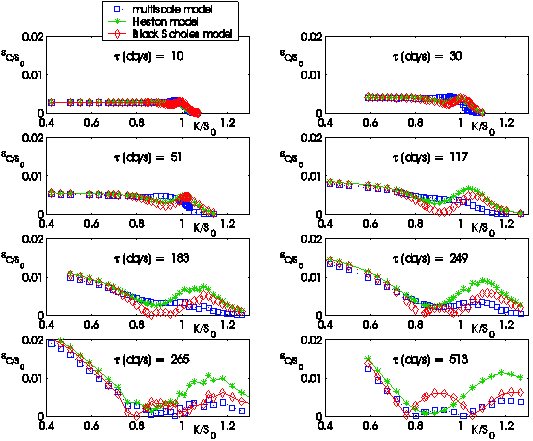
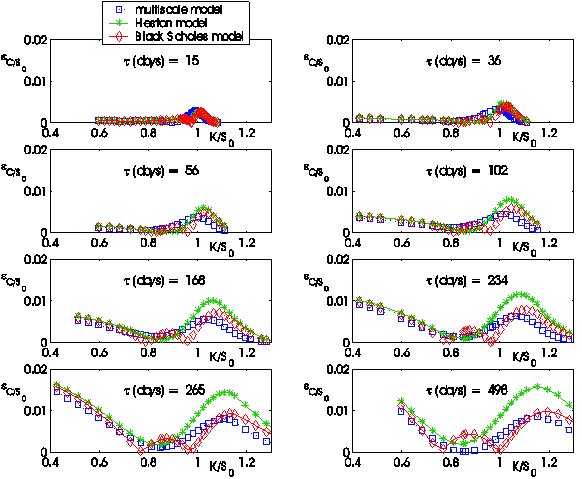
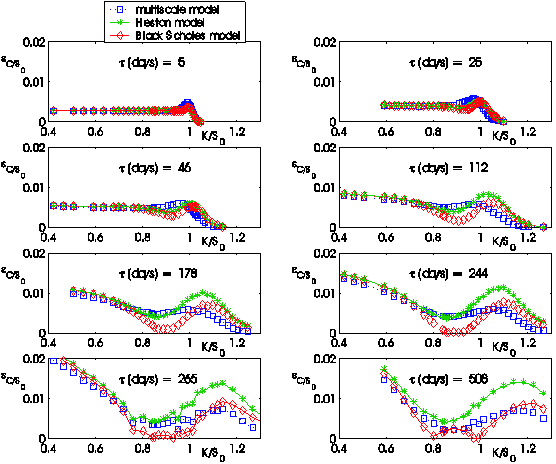
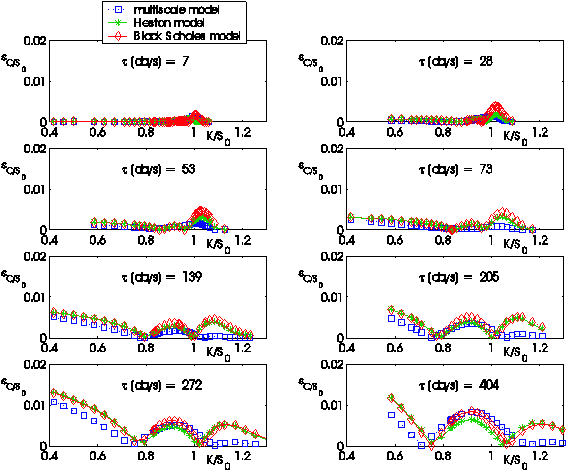
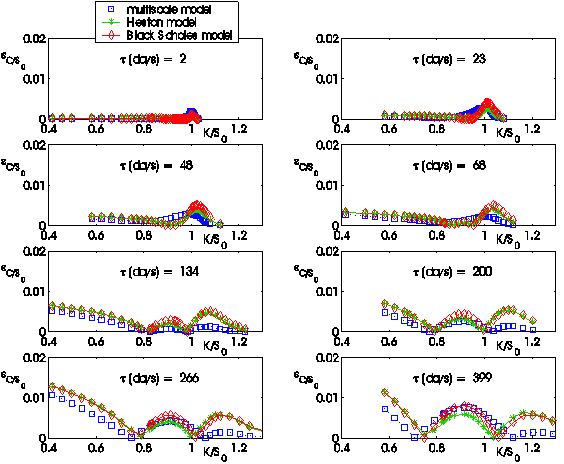
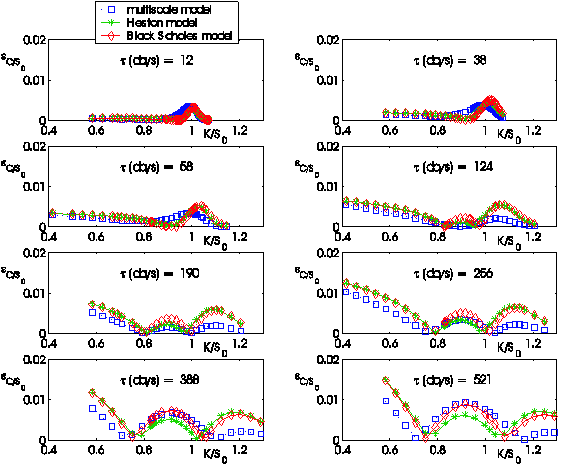
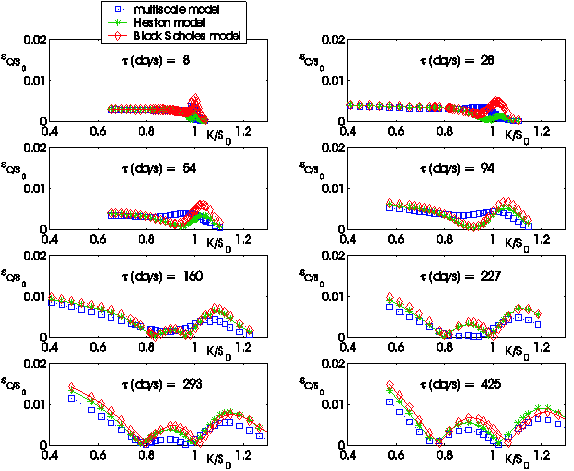
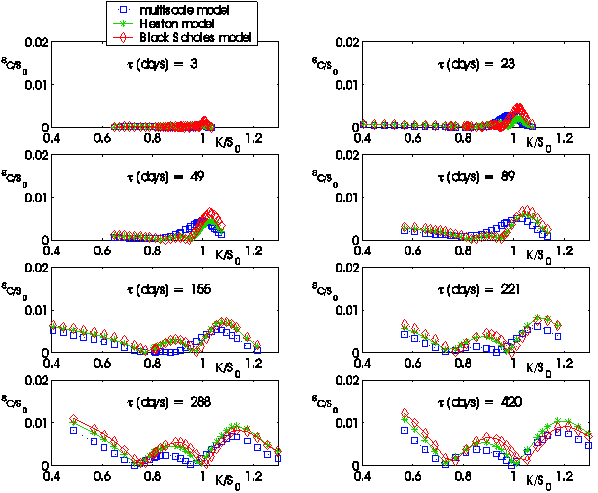
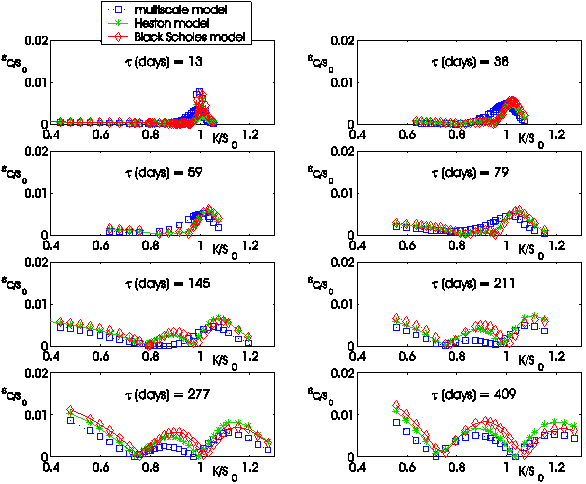
The following figures (i.e. Figures 4, 5, …,12) show the absolute error:
,Ti,Ki) denote respectively the prices
of European call options with strike price Ki and maturity time Ti
(that corresponds to time to maturity ti = Ti-t) observed, generated by
Black Scholes formula, generated by Heston formula and generated by multiscale formula, i=1,2,…, nobs.
The following figures (i.e. Figures 4, 5, …,12) show the absolute error:
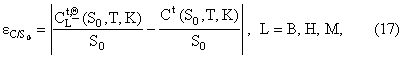
obtained using the three models (L = B(Black
Scholes), H(Heston), M(Multiscale)) as a function of the moneyness
K/S0 = Ki/S0, i = 1,2,¼, nobs, when S0 =![]() is the value of the S&P 500 index at the transaction day
t considered and as a function of the time to maturity ti = Ti-t,
i = 1,2,¼, nobs.
is the value of the S&P 500 index at the transaction day
t considered and as a function of the time to maturity ti = Ti-t,
i = 1,2,¼, nobs.
We
use the parameters estimated on January 3, 2005 (nobs = 281) to
forecast the option prices on January 7 (nobs=282), January 14 (nobs=283),
January 28 (nobs=258), 2005 (see Figures 4, 5, 6). We use the parameters estimated on
June 3, 2005 (nobs = 281) to forecast the option prices on June 7 (nobs= 288), June 14 (nobs
= 291), June 28 (nobs = 278), 2005 (see Figures 7, 8, 9). We use the parameters estimated on
November 3, 2005 (nobs = 303) to forecast the option
prices on November 7 (nobs = 303), November 14 (nobs =
305), November 28 (nobs = 292), 2005 (see Figures 10, 11, 12)
Figures
4, 5,...,12 and the corresponding movies show the behaviour of the absolute
error ![]() committed forecasting
the values of the option prices. We note that the bigger the time to maturity
of the option considered is, the larger is the difference among the behaviour
of the three models and the advantage of using the multiscale model when
compared to the use of the Heston model or of the Black Scholes model.
committed forecasting
the values of the option prices. We note that the bigger the time to maturity
of the option considered is, the larger is the difference among the behaviour
of the three models and the advantage of using the multiscale model when
compared to the use of the Heston model or of the Black Scholes model.
The
numerical experiment presented shows that the solutions of the calibration
problem obtained using the data of January 3, 2005, June 3, 2005 and November
3, 2005 work well when used to forecast the prices of the options in January 7, 14, 28,
June 7, 14, 28 and November 7, 14, 28, 2005 respectively.
|
Figure 4:
January 7, 2005: Absolute error committed on the observed call option prices
using the prices forecasted by the Black Scholes model, the Heston model and
the multiscale model versus moneyness K/S0 |
|
|
Figure 5:
January 14, 2005: Absolute error committed on the observed call option prices
using the prices forecasted by the Black Scholes model, the Heston model and
the multiscale model versus moneyness K/S0 |
|
|
|
|
|
Figure 6:
January 28, 2005: Absolute error committed on the observed call option prices
using the prices forecasted by the Black Scholes model, the Heston model and
the multiscale model versus moneyness K/S0 |
|
|
Figure 7:
June 7, 2005: Absolute error committed on the observed call option prices
using the prices forecasted by the Black Scholes model, the Heston model and
the multiscale model versus moneyness K/S0 |
|
|
Figure 8:
June 14, 2005: Absolute error committed on the observed call option prices
using the prices forecasted by the Black Scholes model, the Heston model and
the multiscale model versus moneyness K/S0 |
|
|
Figure 9:
June 28, 2005: Absolute error committed on the observed call option prices
using the prices forecasted by the Black Scholes model, the Heston model and
the multiscale model versus moneyness K/S0 |
|
|
Figure 10:
November 7, 2005: Absolute error committed on the observed call option prices
using the prices forecasted by the Black Scholes model, the Heston model and
the multiscale model versus moneyness K/S0 |
|
|
Figure 11:
November 14, 2005: Absolute error committed on the observed call option
prices using the prices forecasted by the Black Scholes model, the Heston
model and the multiscale model versus moneyness K/S0 |
|
|
Figure 12:
November 28, 2005: Absolute error committed on the observed call option
prices using the prices forecasted by the Black Scholes model, the Heston
model and the multiscale model versus moneyness K/S0 |
|
[1] F. Black, M. Scholes, “The pricing of options and corporate
liabilities”, Journal of Political Economy, 81, (1973), 637-659.
[2] R. Cont, P. Tankov, Financial modelling with jump processes,
Chapman & Hall/CRC Financial Mathematics Series,
[3] L. Fatone, F. Mariani, M.C. Recchioni, F.
Zirilli: “An explicitly solvable multi-scale stochastic volatility model: option pricing and calibration”, Journal of
Futures Markets, 29(9), (2009), 862-893.
[4] L. Fatone, F. Mariani, M.C. Recchioni, F.
Zirilli: “The calibration of the Heston stochastic volatility model using
filtering and maximum likelihood methods”, in Proceedings of Dynamic Systems and Applications,
G.S.Ladde, N.G.Medhin, Chuang Peng, M.Sambandham Editors, Dynamic Publishers, Atlanta, USA, 5, (2008), 170-181,
(http://www.econ.univpm.it/recchioni/finance/w6).
[5] L. Fatone, F. Mariani, M.C. Recchioni, F.
Zirilli: “Maximum likelihood estimation of the parameters of a system of
stochastic differential equations that models the returns of the index of some
classes of hedge funds”, Journal of Inverse and Ill-Posed Problems, 15,
(2007), 329-362, (http://www.econ.univpm.it/recchioni/finance/w5
contains downloadable software).
[6] J.P. Fouque, G.
Papanicolaou, R. Sircar, K. Solna, “Multiscale
stochastic volatility asymptotics”, SIAM Journal on Multiscale Modeling and
Simulation, 2, (2003), 22-42.
[7] S.L. Heston, “A closed-form solution
for options with stochastic volatility with applications to bond and currency
options”, Review of Financial Studies, 6,
(1993), 327-343.
[8] A. Lipton, Mathematical methods for foreign exchange, World
Scientific Pubblishing Co. Pte. Ltd,
[9] F. Mariani, G. Pacelli, F. Zirilli:
"Maximum likelihood estimation of the Heston stochastic volatility model using
asset and option prices: an application
of nonlinear filtering theory", Optimization
Letters, 2, (2008), 177-222 , (http://www.econ.univpm.it/pacelli/mariani/finance/w1 contains downloadable software).