PAPER:
Determining
a stable relationship between hedge fund index HFRI-Equity and S&P 500
behaviour, using filtering and maximum likelihood
Paolo Capelli, Francesca Mariani, Maria Cristina Recchioni,
Fabio Spinelli, Francesco Zirilli
1.
Abstract
2.
Introduction
3. The
calibration procedure and the formulae used to forecast the log-returns
4. Analysis
of the S&P 500 and HRFI Equity indices (digital
movies)
5. References
Warning: If your browser does not allow you to see the content of this website click here to download a word file that
reproduces the material contained here.
We
test the ability of a stochastic differential model proposed in [5] of forecasting the returns of a long-short equity
hedge fund index and of a market index, that is of the HFRI-Equity index and of
the S&P 500 index respectively. The model is based on the assumptions that
the value of the variation of the log-return of the hedge fund index (HFRI Equity)
is proportional up to an additive stochastic error to the value of the
variation of the log-return of a market index (S&P 500) and that the
log-return of the market index can be satisfactorily modeled using the Heston
stochastic volatility model. The model consists in a system of three stochastic
differential equations, two of them are the Heston stochastic volatility model
and the third one is the equation that models the behaviour of the hedge fund
index and its relation with the market index. The model is calibrated on
observed data using a method based on filtering and maximum likelihood proposed
in [9] and further developed in [4], [5], [6]. The data observed and analyzed go from January
1990 to June 2007, and are monthly data. For each observation time they consist
in the value at the observation time of the log-returns of the HFRI-Equity and
of the S&P 500 indices. The calibration procedure uses appropriate subsets
of the data, that is the data observed in a six months time period. The values
of the HFRI-Equity and of the S&P 500 indices log-returns forecasted by the
calibrated models are compared to the values of the observed indices log-returns.
The result of the comparison is very satisfactory. This website contains some
auxiliary material that helps the understanding of [4].
A more general reference to the work of some of the authors and of their
coauthors in mathematical finance is the website: http://www.econ.univpm.it/recchioni/finance.
2. Introduction
We test on real data the model proposed in [4],
[5] that describes the dynamics of the index of
some classes of hedge funds and of a market index. Let us recall the model
proposed. We denote with R and R+ the set of real numbers and of
positive real numbers respectively, with t the time variable, and with (xt,zt,vt),
t > 0, a stochastic process, we will interpret xt,
t > 0, as the log-return of a market index, zt,
t > 0, as the log-return of the index of a class of
hedge funds and vt, t > 0, as the stochastic variance of the
market index. We consider the S&P 500 index as market index and the
HFRI-Equity hedge fund index as index of a class of hedge funds, that is the
class of ``long-short equity" hedge funds. The model proposed in [4], [5] can be used with
several other choices for the meaning of the indices. In [4],
[5] the
dynamics of the stochastic process (xt,zt,vt),
t > 0, is modeled by the following system of
stochastic differential equations:
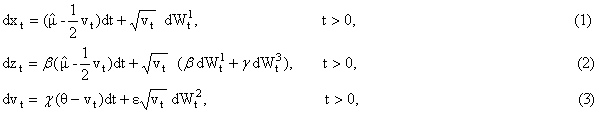

where ![]() , b, g, c, q, e are
constants,
, b, g, c, q, e are
constants, ![]() ,
, ![]() ,
, ![]() , t ³ 0, are standard Wiener processes such that W01=W02= W03
=0, and d
, t ³ 0, are standard Wiener processes such that W01=W02= W03
=0, and d![]() , d
, d![]() , d
, d![]() , t>0, are their stochastic differentials. Moreover we assume that:
, t>0, are their stochastic differentials. Moreover we assume that:
|
|
where
< · > denotes the expected value of ·, and
the quantities r1,2, r1,3, r2,3 Î [-1,1] are constants known as
correlation coefficients. We note that the autocorrelation coefficients of dWit,
t>0, i = 1,2,3 are equal to one.
Equations
(1), (3) are the well known Heston stochastic volatility model [8]. This model was introduced with the aim of overcoming
some limitations of the Black Scholes model [3] that
are pointed out by market data such as, for example, the assumption of constant
volatility. Let St, t > 0, be the price at time t of an
asset, the Heston model (1), (3) describes satisfactorily the dynamics of the log-return
xt = log(St/S0), t > 0, of the asset and of its stochastic variance vt, t > 0. Note that
x0 = log1 = 0 =![]() and that since zt, t>0, is a log-return a
similar statement holds for z0, that is z0 = 0 =
and that since zt, t>0, is a log-return a
similar statement holds for z0, that is z0 = 0 =![]() . A systematic data analysis has shown that the Heston stochastic
volatility model is well suited to model the behaviour of several market indices
such as, for example, the S&P 500 index, the Dow-Jones Industrials index
and the Nasdaq Composite index (see [7]). We note
that equation (3) is known as equation of the mean-reverting process with speed c and parameters q and e. The initial stochastic variance
. A systematic data analysis has shown that the Heston stochastic
volatility model is well suited to model the behaviour of several market indices
such as, for example, the S&P 500 index, the Dow-Jones Industrials index
and the Nasdaq Composite index (see [7]). We note
that equation (3) is known as equation of the mean-reverting process with speed c and parameters q and e. The initial stochastic variance ![]() is a random variable
that we assume to be concentrated in a point, that we continue to denote
with
is a random variable
that we assume to be concentrated in a point, that we continue to denote
with ![]() , with probability one.
, with probability one.
We
note that the model (1), (2), (3) introduced
in [5] and analyzed on real data in [4]
is obtained adding to the Heston stochastic volatility model (1), (3)
a third equation, that is equation (2), that describes the behaviour of
the log-return of the index of some
classes of hedge funds. In fact statistical studies, such as [10], of the
time series of the data relative to the
log-returns of the indices of several classes of hedge funds have shown
that the log-returns of the indices of some classes of hedge funds are related
to the log-returns of the S&P 500 index. In particular in [10] some discrete time models are proposed to
study nine different classes of hedge funds.
The model proposed in [10] to describe the dynamics of the log-return of the index of the
“long-short equity” class of hedge funds is based on the assumption that up to
a stochastic additive error there exists a kind of direct proportionality
between the behaviour of the variation of the log-return of the index of the “long-short equity"
class of hedge funds and the variation
of the log-return of the S&P500 index. In [10]
this assumption is supported by convincing empirical evidence. So that
interpreting zt, t>0, as the log-return at time t of an index
of the “long-short equity" class of
hedge funds, that is the HFRI-Equity
index, xt, t>0, as the log-return at time t of the S& P500
index and vt, t>0, as the stochastic variance of xt, t>0, the
system of stochastic differential equations (1), (2), (3) obtained
coupling the Heston model (1), (3) with
equation (2) can be seen as a reasonable translation in continuous time of the model proposed in [10]. In fact equation (2) states that dzt
is given by the sum of b dxt and a random disturbance given
by g![]() dWt3.
dWt3.
The calibration
problem of model (1), (2), (3) can be stated as follows: given a discrete
set of time values t=ti, i=0,1,…,n, such that t0=0, ti<ti+1,
i=0,1,…,n-1, and the observation ![]() of the log-returns of
the market and of the hedge fund
indices, that is the observation of (xt,zt), at time t=ti,
i=0,1,…,n, determine the values of the parameters appearing in (1), (2), (3), of the correlation
coefficients r1,2, r1,3, r2,3
and of the
initial stochastic variance
of the log-returns of
the market and of the hedge fund
indices, that is the observation of (xt,zt), at time t=ti,
i=0,1,…,n, determine the values of the parameters appearing in (1), (2), (3), of the correlation
coefficients r1,2, r1,3, r2,3
and of the
initial stochastic variance ![]() . That is the
parameters (including the correlation coefficients) and the unknown initial
condition component of model (1), (2),
(3) that we want to estimate starting from the observations are:
. That is the
parameters (including the correlation coefficients) and the unknown initial
condition component of model (1), (2),
(3) that we want to estimate starting from the observations are: ![]() , q, c, e, g, b, r1,2, r1,3, r2,3 and
, q, c, e, g, b, r1,2, r1,3, r2,3 and ![]() .
.
Note
that the choice t0=0 corresponds to choosing the origin of the time
axis in the first observation time where we choose ![]() =(0,0). Note that the origin of the time axis can be moved at our convenience in the time
series of the data without changing substantially the problem considered.
=(0,0). Note that the origin of the time axis can be moved at our convenience in the time
series of the data without changing substantially the problem considered.
In
order to study time series of real data the calibration problem
of model (1), (2), (3) stated
previously has been solved using the approach suggested in [5] based on the methods of filtering and maximum likelihood. This approach was introduced in the context of mathematical finance in [9] and
further developed in [5], [6].
Going into details, we suppose that at discrete times 0=t0<t1<t2<…<tn<tn+1
=+¥,
the log-return of the
S&P500 index and the
log-return of the HFRI Equity index are
observed and let Ft=
{(![]() ,
,![]() ) : ti £t}, t>0, be the set of the observations
available at time t>0 of the
log-returns of the market index xt and of the log-returns of the
index of the hedge funds zt. We assume that the observations are
error free, that is we assume that
) : ti £t}, t>0, be the set of the observations
available at time t>0 of the
log-returns of the market index xt and of the log-returns of the
index of the hedge funds zt. We assume that the observations are
error free, that is we assume that ![]() =
=![]() ,
, ![]() =
=![]() , i=0,1,…,n. Let
, i=0,1,…,n. Let ![]() be the vector of the
model parameters (including the correlation coefficients) and of the initial
stochastic variance, where the superscript T denotes the transposed
operator. We use the notation t0 =0 and F0={(
be the vector of the
model parameters (including the correlation coefficients) and of the initial
stochastic variance, where the superscript T denotes the transposed
operator. We use the notation t0 =0 and F0={(![]() )}to simplify some of the formulae that follow.
)}to simplify some of the formulae that follow.
We
determine the joint probability density function of having xt=x, zt=z
and vt =v at time t>0 conditioned to the observations contained in Ft, t>0, and to the initial condition (6). Note that the initial conditions (4), (5)
are already contained in Ft, t>0. This joint probability
density function is determined solving a filtering problem that has been
presented in [9], [5], [6].
In [5] the calibration problem is translated in a maximum
likelihood optimization problem (see Section 3). We apply
these methods to analyze real data. In particular we consider the time series of monthly data of the S&P
500 and of the HFRI-Equity indices covering a period of 210 months going from
January 31, 1990 to June 30, 2007.
The observation times will be denoted with t=![]() , i=1,2,…,210, and we introduce t=
, i=1,2,…,210, and we introduce t=![]() corresponding to December 31, 1989. From these data we
derive the corresponding time series of the log-returns. We have applied the calibration procedure
described above using as data the data contained in a window of six consecutive observation times (that is a window covering the data relative to a period of six
months) corresponding to twelve data,
that is the window corresponding to the data
(
corresponding to December 31, 1989. From these data we
derive the corresponding time series of the log-returns. We have applied the calibration procedure
described above using as data the data contained in a window of six consecutive observation times (that is a window covering the data relative to a period of six
months) corresponding to twelve data,
that is the window corresponding to the data
(![]() ,
,![]() ) observed at time t=
) observed at time t=![]() , i=k, k+1,…,k+5 for some k. Note that in the calibration
problems derived from the data time series the origin of the time axis is
translated to the first observation time contained in the data window
considered. The numerical results
obtained considering the data windows
associated to the choices k=0,1,…,205 are presented in Section
4 and they show that the solutions of the calibration problems considered are
really associated to the data time series, that is they are “stable” when the time window of the data used in the
calibration is shifted. In fact as shown
in Figures 1, 2, 3 the solution of the calibration problem as a function of the time window of the data
used in the calibration can be grouped
into three sets associated to the data
of three non overlapping time periods and in
these three sets the parameters
(including the correlation coefficients)
and the initial stochastic variance found
are approximately constants (see Section 4 for further details). After calibrating the model using the data belonging to
a six month window we use the resulting estimate of the parameters and
of the initial stochastic variance to
forecast the market and the hedge fund
indices one, three and six months in the future counting as future the time after the last observation time
contained in the data window used in the calibration. The forecasted values of the market and of the
hedge fund indices are obtained using some formulae derived in [5] that
translate to the case of model (1), (2), (3)
standard formulae of filtering theory.
We perform this forecasting exercise moving the data window along the data time
series step by step, at each step
we discard the observations relative to the first observation time of the
window and we insert the observations relative to the next observation time
after the window, that is in the previous notation we consider the data windows
associated to k=0,1,...,205.The quality of these forecasts is established a
priori using filtering theory and a posteriori comparing the forecasted
values with the historical data. The results obtained suggest that the model proposed
describes satisfactorily the
data, and that it is able to produce high quality forecasts of the value of the hedge fund index log-return
several months in the future. Forecasts of approximately the same quality are
obtained for the log-returns of the market index. We remark that the forecasts
that are expected to be good a priori on the basis of filtering theory are a
posteriori actually better than the average forecast.
, i=k, k+1,…,k+5 for some k. Note that in the calibration
problems derived from the data time series the origin of the time axis is
translated to the first observation time contained in the data window
considered. The numerical results
obtained considering the data windows
associated to the choices k=0,1,…,205 are presented in Section
4 and they show that the solutions of the calibration problems considered are
really associated to the data time series, that is they are “stable” when the time window of the data used in the
calibration is shifted. In fact as shown
in Figures 1, 2, 3 the solution of the calibration problem as a function of the time window of the data
used in the calibration can be grouped
into three sets associated to the data
of three non overlapping time periods and in
these three sets the parameters
(including the correlation coefficients)
and the initial stochastic variance found
are approximately constants (see Section 4 for further details). After calibrating the model using the data belonging to
a six month window we use the resulting estimate of the parameters and
of the initial stochastic variance to
forecast the market and the hedge fund
indices one, three and six months in the future counting as future the time after the last observation time
contained in the data window used in the calibration. The forecasted values of the market and of the
hedge fund indices are obtained using some formulae derived in [5] that
translate to the case of model (1), (2), (3)
standard formulae of filtering theory.
We perform this forecasting exercise moving the data window along the data time
series step by step, at each step
we discard the observations relative to the first observation time of the
window and we insert the observations relative to the next observation time
after the window, that is in the previous notation we consider the data windows
associated to k=0,1,...,205.The quality of these forecasts is established a
priori using filtering theory and a posteriori comparing the forecasted
values with the historical data. The results obtained suggest that the model proposed
describes satisfactorily the
data, and that it is able to produce high quality forecasts of the value of the hedge fund index log-return
several months in the future. Forecasts of approximately the same quality are
obtained for the log-returns of the market index. We remark that the forecasts
that are expected to be good a priori on the basis of filtering theory are a
posteriori actually better than the average forecast.
3. The calibration procedure and the formulae used to forecast the
log-returns
Let us
formulate the calibration problem and let us give some formulae used to
forecast the log-returns xt, zt and the stochastic
variance vt, t > 0, solution of problem (1), (2), (3),
(4), (5), (6). Moreover we give some
formulae that can be used to evaluate “a priori” the quality of the forecasted
values of the log-returns (and of the stochastic variance) as explained in Section 4.
Let us consider the joint
probability density function ![]() =
=![]() (x,z,v,t|Ft, Q), (x,z,v) Î R×R×R+, t > 0, of having xt = x, zt
= z, vt = v given Ft, t > 0, and Q. Remind that
(x,z,v,t|Ft, Q), (x,z,v) Î R×R×R+, t > 0, of having xt = x, zt
= z, vt = v given Ft, t > 0, and Q. Remind that ![]() =
=![]() = 0. The joint probability density function
= 0. The joint probability density function ![]() is the solution of a
filtering problem, and in [4] , [5] we have shown that the function
is the solution of a
filtering problem, and in [4] , [5] we have shown that the function ![]() is given by:
is given by:
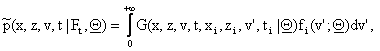
![]() i=0,1,…,n, (10)
i=0,1,…,n, (10)
where G(x,z,v,t,x¢,z¢,v¢,t¢| Q), (x,z,v), (x¢,z¢,v¢) Î R×R×R+, t, t¢ > 0, t-t¢ > 0, is the fundamental solution of
the Fokker Planck equation associated to the system of stochastic differential
equations (1), (2), (3), and we have
for: i = 0:
|
|
|||||||||
|
|
|
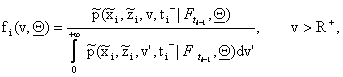 (12)
(12)
where d(.) is the Dirac’s delta and ![]() denotes the left limit t that goes to ti.
denotes the left limit t that goes to ti.
In order to determine the
vector Q we solve the calibration problem, that is we
solve the optimization problem:
|
|
where the
log-likelihood function F( Q) is given by:
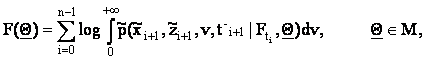 (14)
(14)
and the set of the admissible vectors M
is given by:
![]() . (15)
. (15)
We
maximize the function (14) using as optimization method a variable metric
steepest ascent method. This method is a kind of steepest ascent method based
on an iterative procedure that searches the maximum likelihood estimate Q*,
solution of (13), beginning from an initial guess Q0 Î M and that for k = 1,2,¼ generates at step k a feasible point Qk Î M satisfying the inequality F(Qk) > F( Qk-1), that is the objective function is
monotonically increasing along the sequence {Qk}, k = 0,1,¼. In the numerical experience presented in Section
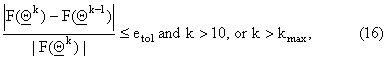
where etol, kmax are
positive constants that will be chosen later.
We note that the log-likelihood function (14)
is only one possible choice between many
other possibilities and that the
constraints contained in (15) that define M express some elementary properties satisfied by model (1), (2), (3).
Given
the joint probability density function ![]() (x,z,v,t|Ft, Q), (x,z,v) Î R×R×R+, t ³ 0, we can forecast the values of
the market index log-return, of the hedge fund index log-return xt,
zt, t > 0, t ¹ ti,
i = 0,1,¼,n, and of the stochastic variance vt, t > 0, using respectively the mean values
(x,z,v,t|Ft, Q), (x,z,v) Î R×R×R+, t ³ 0, we can forecast the values of
the market index log-return, of the hedge fund index log-return xt,
zt, t > 0, t ¹ ti,
i = 0,1,¼,n, and of the stochastic variance vt, t > 0, using respectively the mean values ![]() t| Q,
t| Q, ![]() t| Q,
t| Q, ![]() t| Q, t > 0, conditioned to the observations contained in Ft, t > 0, of the random variables xt, zt, vt,
t > 0, that is:
t| Q, t > 0, conditioned to the observations contained in Ft, t > 0, of the random variables xt, zt, vt,
t > 0, that is:
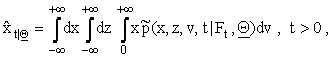 (17)
(17)
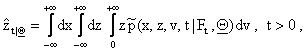 (18)
(18)
![]()
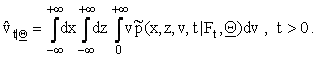 (19)
(19)
Note that in Section 4 we
are interested in forecasting xt, zt, vt when t>tn and that this
corresponds to the genuine meaning of the word “forecast”.
As shown in
[5] from (10), (12), (17), (18), (19), we have:

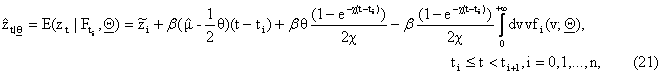
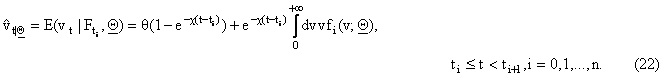
Remind
that we use the notation tn+1 = +¥. Note that it
is easy to see that, as it should be, we have: ![]() ,
, ![]() , i = 0,1,¼,n. The quality of the forecasted
values
, i = 0,1,¼,n. The quality of the forecasted
values ![]() depends from the variance of the random variables xt,
zt, vt, t>0, conditioned
to the observations, that is we can estimate the quality of the estimates (20),
(21), (22) computing respectively the quantities:
depends from the variance of the random variables xt,
zt, vt, t>0, conditioned
to the observations, that is we can estimate the quality of the estimates (20),
(21), (22) computing respectively the quantities:
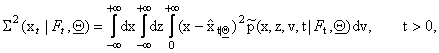 (23)
(23)
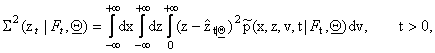 (24)
(24)
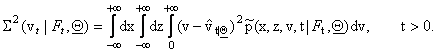 (25)
(25)
The estimates (20), (21), (22) are expected to
be good, when the variances (23), (24), (25) are small. In [5] some formulae similar to (20), (21), (22) are
derived from (23), (24), (25).
4. Analysis of the S&P 500
and HRFI Equity indices
Let us present the results obtained applying
the procedure described in the previous Sections to the historical series of
210 monthly data relative to the variation DIx,i
of the S&P 500 index Ix,i, at time t=![]() , i = 1,2,¼,210, and to the variation DIz,i of the HFRI-Equity index Iz,i, at time t=
, i = 1,2,¼,210, and to the variation DIz,i of the HFRI-Equity index Iz,i, at time t=![]() , i=1,2,…,210 (see formulae (30), (31)). The data cover the
period of 210 months going from January 31, 1990 to June 30, 2007. The
observation dates t =
, i=1,2,…,210 (see formulae (30), (31)). The data cover the
period of 210 months going from January 31, 1990 to June 30, 2007. The
observation dates t =![]() , i = 1,2,¼, 210 are the last day of the month
(i.e. January 31, February 28, March 31, April 30, May 31, June 30, July 31,
August 31, September 30, October 31, November 30, December 31) of the period
January 1990, June 2007. We have added to these data the observation at date t
=
, i = 1,2,¼, 210 are the last day of the month
(i.e. January 31, February 28, March 31, April 30, May 31, June 30, July 31,
August 31, September 30, October 31, November 30, December 31) of the period
January 1990, June 2007. We have added to these data the observation at date t
=![]() corresponding to December 31, 1989. We choose Ix,0=Iz,0=1 and
corresponding to December 31, 1989. We choose Ix,0=Iz,0=1 and ![]() ,
, ![]() . First of all we have manipulated the data DIx,i, DIz,i, i = 1,2,¼,
. First of all we have manipulated the data DIx,i, DIz,i, i = 1,2,¼, ![]() , i = 1,¼, 210, of the S&P 500 index and
of the observed log-return
, i = 1,¼, 210, of the S&P 500 index and
of the observed log-return ![]() , i = 1,¼,210, of the HFRI-Equity index. To visualize and eventually download the data click here Table
1 .
, i = 1,¼,210, of the HFRI-Equity index. To visualize and eventually download the data click here Table
1 .
We
have used the following recursive formulae to construct the log-returns (i.e.
the last two columns of Table 1):
![]()
![]()
where as mentioned above ![]() ,
, ![]() correspond to the log-returns at time t =
correspond to the log-returns at time t =![]() (December 31, 1989) that have been chosen equal to zero.
(December 31, 1989) that have been chosen equal to zero.
The
indices Ix,0, Iz,0 have been assumed to be equal one and Ix,i,
Iz,i, i = 1,2,¼, 210 are related to the monthly
log-returns ![]() ,
, ![]() , i = 1,2,¼,210, defined in (26), (27) by the
following formulae:
, i = 1,2,¼,210, defined in (26), (27) by the
following formulae:
|
(28) |
|
(29) |
|
(30) |
|
(31) |
We consider a window of six consecutive observation
times (that is a window covering a time period of six months) corresponding to
twelve data and we move from a window to the next one removing the data
relative to the first observation time of the window and adding the data
corresponding to the observation time that follows the last observation time of
the window. That is the j-th window contains the data (![]() ,
, ![]() ), i = 1,2,¼,6, j = 1,2,¼,206. For each data window we solve the calibration problem (13). We
have solved 206 calibration problems. Remind that in the solution of each
calibration problem, coherently with the statement of the problem given in the
Introduction, we translate appropriately the origin of the time axis.
), i = 1,2,¼,6, j = 1,2,¼,206. For each data window we solve the calibration problem (13). We
have solved 206 calibration problems. Remind that in the solution of each
calibration problem, coherently with the statement of the problem given in the
Introduction, we translate appropriately the origin of the time axis.
The
data analysis presented investigates the following two problems.
Problem 1: understand
if the calibration procedure described in Section 2 to determine the value of
the vector Q, that is the maximum likelihood
problem (13), gives values of Q that are really associated to the
data time series, that is values of Q that are approximately constant
when we change the data window used in the calibration. If this is the case the
values of Q determined by the calibration
procedure are not an artifact of the computational procedure used to determine
them. Note that despite the fact that the stochastic variance is the solution
of a stochastic differential equation it is reasonable to assume that the
stochastic variance is approximately constant over long periods of time and
that it changes abruptly from time to time.
Problem 2: evaluate
the capability of the models corresponding to the values of Q determined with the calibration procedure of forecasting the values
of xt, zt in the future, that is of forecasting using the
formulae (20), (21) the values xt,
zt relative to observation times posterior to the observation times
contained in the data window used to estimate the vector Q. This capability is evaluated a
priori using formulae (23), (24) and established a posteriori comparing the
forecasted values with the observations actually made. Note that Problem 2 is considered
since Problem 1 is solved positively.
Investigation
of Problem 1
As said previously
we have solved 206 calibration problems relative to the 206 data windows
described above determining 206 values of the vector Q. In the solution of the 206 maximization problems (13) we have chosen
the initial guess of the maximization procedure to be always the same vector
and in the stopping criterion (16) we have chosen etol= 5·10-4 and kmax
= 10000.
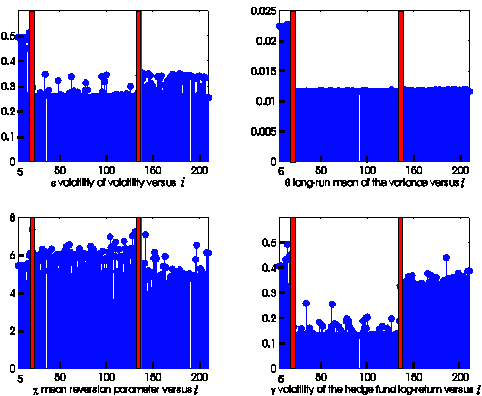
Figures
1, 2, 3 show (in ordinate) the
components of the vector Q obtained solving the maximum
likelihood problem (13) as a function of i (in abscissa), where i is the index
value of the last observation time ![]() of the data window
considered. That is the vector Q obtained using a given data window
is associated to the index of the last observation time of the data contained
in the window.
of the data window
considered. That is the vector Q obtained using a given data window
is associated to the index of the last observation time of the data contained
in the window.
Figure 1: Reconstruction of the parameters e, q, c, g (in ordinate)
of the model (1), (2), (3) as a function of the index value of the last
observation time contained in the data window considered (in abscissa)
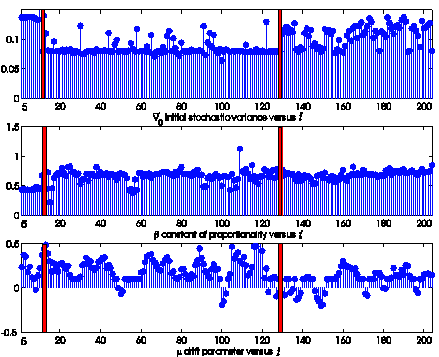
Figure 2: Reconstruction of the initial stochastic
variance ![]() and of the parameters b, m (in ordinate) of the model (1), (2), (3) as a
function of the index value of the last observation time contained in the data
window considered (in abscissa)
and of the parameters b, m (in ordinate) of the model (1), (2), (3) as a
function of the index value of the last observation time contained in the data
window considered (in abscissa)
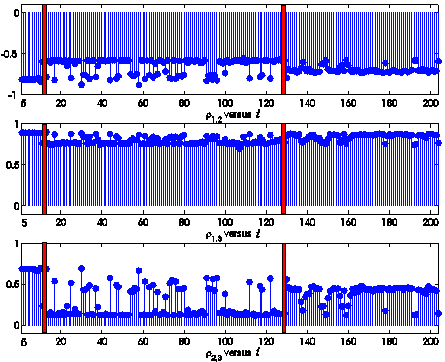
Figure 3:
Reconstruction of the correlation coefficients r1,2, r1,3, r2,3 (in ordinate) of the model (1), (2),
(3) as a function of the index value of the last observation time contained in
the data window considered (in abscissa)
Figures
1, 2 and 3 show that the parameters e, g, the initial stochastic variance ![]() and the correlation
coefficients r1,2 and r2,3 as a function of i are approximately given by
piecewise constant functions. In particular two observation times (marked with the
red bars in the Figures) where the piecewise constant functions jump are
evidenced, the first one is located approximately after the first year of
observation (October 31, 1990) and the second one is located approximately after
ten years of observations (October 31, 2000). The data analysis carried out and
illustrated in Figures 1, 2, 3 shows that the data can be divided into three
periods:
and the correlation
coefficients r1,2 and r2,3 as a function of i are approximately given by
piecewise constant functions. In particular two observation times (marked with the
red bars in the Figures) where the piecewise constant functions jump are
evidenced, the first one is located approximately after the first year of
observation (October 31, 1990) and the second one is located approximately after
ten years of observations (October 31, 2000). The data analysis carried out and
illustrated in Figures 1, 2, 3 shows that the data can be divided into three
periods:
- Period 1: this period (from the
beginning of the time series up to the first red bar) is very small and
covers the period going from December 31, 1989 to October 31, 1990;
- Period 2: this period (between
the first and the second red bar) is quite long and covers the period going from November 30, 1990 to October 31,
2000;
- Period 3: this period (after
the second red bar until the end of the time series) covers the period going from November 30, 2000 to June 30, 2007.
That
is the data analysis carried out solving the 206 calibration problems
considered shows that the vectors Q determined by the calibration
procedure can be considered approximately constants in each one of the three
Periods mentioned above.
Moreover
in Figure 3 we can see that the correlation coefficient r1,3 that
measures the correlation between two of the stochastic differentials present in
the equations of the log-return of the S&P 500 index and of the log-return
of the hedge fund HFRI-Equity index, is almost constant and approximately equal
to one over the entire observation period. This fact seems to confirm the
validity of model (1), (2), (3) that assumes that the behaviour of the hedge
fund HFRI-Equity index depends strongly from the behaviour of the S&P 500
index. Furthermore the fact that the parameter b is
substantially constant (exception made when we go from Period 1 to Period 2
where b goes approximately from 0.5 to 0.7) confirms
the assumption of the existence of a kind of
“proportionality” between the variations of the HFRI-Equity hedge
fund index and of the S&P 500 index log-returns.
We
can conclude that the data analysis presented shows a convincing evidence of
the fact that the values of the vector Q determined by the maximum
likelihood procedure (13) are really associated to the data time series and
supports some of the assumptions made to build model (1), (2), (3).
Investigation
of Problem 2
The
second problem addressed in the data analysis is the investigation of the
quality of the forecasted values of the log-returns of the indices obtained
using model (1), (2), (3) and the values
of Q shown in
Figures 1, 2, 3 determined solving the calibration problems. That is, we use
the values of the vectors Q determined solving the maximum
likelihood problems and formulae (20), (21) to forecast the values of the
returns xt and zt and of the increments of the
HFRI-Equity index![]() =
= 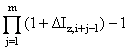 , i=5,6,…,210-m, m = 1,2,¼,6, that is one month, two months,... up to six months in
the future. Note that here “future” means the time that follows the last
observation contained in the data window used to estimate the vector Q.
, i=5,6,…,210-m, m = 1,2,¼,6, that is one month, two months,... up to six months in
the future. Note that here “future” means the time that follows the last
observation contained in the data window used to estimate the vector Q.
Let
Ntot be a positive integer that denotes the number of forecasted values m months in the future of the returns of the S&P 500 index and of
the HFRI-Equity index used in this study. Note that below we will choose Ntot
independent of m, m=1,2,…,6. The forecasted values are compared with the
historical data and the following quantities have been defined to measure the
accuracy of the forecasted values:
where the
quantities ![]() ,
, ![]() are given by:
are given by:

where![]() ,
, ![]() and
and ![]() , i = 1,2,¼,Ntot , m=1,2,…,6, are the observed values (real data) and
, i = 1,2,¼,Ntot , m=1,2,…,6, are the observed values (real data) and ![]()
![]() ,
, ![]() are the corresponding
forecasted values m months in the future, m=1,2,…,6 and
are the corresponding
forecasted values m months in the future, m=1,2,…,6 and![]() , i=1,2,…,Ntot, j=1,2,…m, are the variations of
the index Iz,4+i+j-1 computed using the forecasted values
, i=1,2,…,Ntot, j=1,2,…m, are the variations of
the index Iz,4+i+j-1 computed using the forecasted values ![]() , i=1,2,…, Ntot, m=1,2,…,6. Remind that t =
, i=1,2,…, Ntot, m=1,2,…,6. Remind that t =![]() , i = 1,2,¼,210 are the observation times where
the historical data are given. Finally we have computed the mean value of the
quantities
, i = 1,2,¼,210 are the observation times where
the historical data are given. Finally we have computed the mean value of the
quantities ![]() , i = 1,2,¼,Ntot, that is sm
=
, i = 1,2,¼,Ntot, that is sm
= 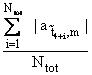 , m=1,2,…,6.
, m=1,2,…,6.
In
Table 2 we show the values of the quantities ex,m, ez,m, evar,m and
sm as a function of the forecasting period m (one, two,..., six
months in the future) and we consider Ntot = 200 observation times.
The choice Ntot = 200 depends from the fact that when we forecast
the values of the two indices up to six months in the future using data windows
of six months and a time series of 211 monthly observation times (remind that
we have also the couple (![]() ,
,![]() ) at time t=
) at time t=![]() ), we cannot forecast values corresponding to the first six
observation times and we cannot check the quality comparing with the historical
data of the forecasted values obtained using as data windows containing data
corresponding to the last six observation times so that we can consider the
last observation time of the windows indexed by i=5,6,…,204, that is we can
consider Ntot = 204-5+1 = 200
dates (i.e. t=
), we cannot forecast values corresponding to the first six
observation times and we cannot check the quality comparing with the historical
data of the forecasted values obtained using as data windows containing data
corresponding to the last six observation times so that we can consider the
last observation time of the windows indexed by i=5,6,…,204, that is we can
consider Ntot = 204-5+1 = 200
dates (i.e. t=![]() ,
, ![]() , ….,
, …., ![]() ) such that “starting”
from them we can compute forecasted values six months in the future that
can be compared with the historical data.
) such that “starting”
from them we can compute forecasted values six months in the future that
can be compared with the historical data.
We
note that the quantities ex,m, ez,m are the mean values of the relative errors
committed on the forecasted values of the log-returns xt, zt
of the S& P 500 index and of the HFRI-Equity index respectively and that
for m=1,2,…,6, evar,m is the mean value of the absolute errors
committed on the forecasted values of the HFRI-Equity index Iz,t = ![]() m months in the
future, that is one month, two months, ..., up to six months in the future.
m months in the
future, that is one month, two months, ..., up to six months in the future.
Table 2: Quality indices of the forecasted values
|
Forecasting period m |
|
|
|
|
|
1 month |
0.1271 |
0.0214 |
0.0202 |
0.0217 |
|
2 months |
0.1739 |
0.0331 |
0.0327 |
0.0365 |
|
3 months |
0.1976 |
0.0397 |
0.0435 |
0.0499 |
|
4 months |
0.2226 |
0.0478 |
0.0530 |
0.0631 |
|
5 months |
0.2425 |
0.0577 |
0.0633 |
0.0770 |
|
6 months |
0.2967 |
0.0616 |
0.0715 |
0.0907 |
Finally we show the
histograms of the absolute errors committed on the quantities at,m, that
is the histograms of the values taken by the function nm(t) =![]() , t =
, t =![]() , i = 1,2,¼,Ntot, m = 1,3,6 (see
Figures 4, 5, 6).
, i = 1,2,¼,Ntot, m = 1,3,6 (see
Figures 4, 5, 6).
Figure 4: Histogram of n1(t)
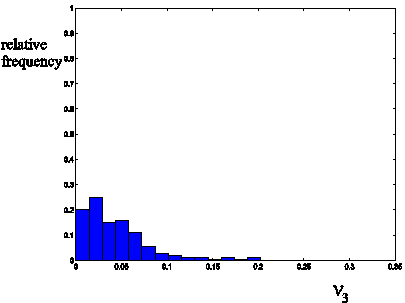
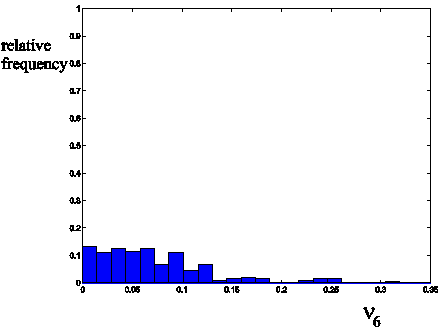
Table 3 shows the observations and the forecasted
values. Note that in Table 3 in the first 46 observation times some
values are evidenced in blue colour. These values are some of the most
satisfactory forecasted values of at,m,
m = 1,6 one month and six months in the future. We have computed the
conditioned variance of the state variable zt (formula (24))
corresponding to these forecasted values of the HFRI-Equity index. We observe that the
conditioned variances relative to the forecasted values of the returns one
month or six months in the future marked in blue are significantly smaller than
the remaining ones. For example, while the mean value of the conditioned
variances of the forecasted values of the returns of the HFRI-Equity index one
month in the future is 1.27·10-2 the value of the variances of the
forecasted values marked in blue (in time order) are 7.4·10-3,
4.4·10-3, 6.1·10-3, that is the conditioned variance of
the blue forecasts is reduced of approximately a factor 0.5 with respect to its
mean value. The same happens in the case of the forecasted values six months in
the future where the mean value of the conditioned variance is 2.5·10-2
and the conditioned variances of the forecasted values marked in blue (in time
order) are 9.94·10-3, 9.96·10-3, 1.18·10-2 and
1.23·10-2. That is also in this last case the conditioned variances
of the forecasted values marked in blue are reduced of approximately a factor
0.5 with respect to its mean value. This
fact observed in the high quality forecasts contained in the first 46
observation times is confirmed when we look to the entire data time series. We
have limited the study of the high quality forecasts to the first 46
observation times for simplicity. Similar results are obtained studying the
forecasted values of the S&P 500 index.
This
analysis shows that the conditioned variance allows us to assign a priori a
degree of reliability to the corresponding forecasted value, that is: a small
conditioned variance actually corresponds to a great degree of reliability of
the corresponding forecasted value. This fact may be of great relevance in
practical situations since using the conditioned variances we can evaluate a
priori the quality of the forecasts of
the HFRI-Equity index.
We conclude showing two
digital movies concerning the forecasting problem.
The
first movie shows
the forecasted values one month , three months and six months in the
future of the SP&500 index and of
the HFRI Equity hedge fund index in comparison with the observed values, that
is the point ![]() one, three, six months
in the future is shown in the cartesian plane and compared with the
corresponding observed points when the
time t ranges in the observation period that goes from May 31, 1990 to December 31,
2006.
one, three, six months
in the future is shown in the cartesian plane and compared with the
corresponding observed points when the
time t ranges in the observation period that goes from May 31, 1990 to December 31,
2006.
Click here to see the first movie
The
second movie shows how the conditioned
variances of the indices (see formulae (23), (24) ) can be used as a priori
estimates of the quality of the forecasted values. In the movie we show the forecasted values ![]() of the variations of
the log-return of the HFRI hedge fund index, the corresponding historical
variations
of the variations of
the log-return of the HFRI hedge fund index, the corresponding historical
variations ![]() , i=1,2,…,Ntot ,m=1,3,6, and the corresponding
conditioned variances. Note that when the conditioned variance of zt
is small the quality of the forecasted
value is high.
, i=1,2,…,Ntot ,m=1,3,6, and the corresponding
conditioned variances. Note that when the conditioned variance of zt
is small the quality of the forecasted
value is high.
Click here to see the second movie
5. References
[1] Y. Ait-Sahalia, R. Kimmel, Maximum
likelihood estimation of stochastic volatility models, Journal of Financial
Economics, 83 (2007), 413-452.
[2] D.S. Bates, Maximum
likelihood estimation of latent affine processes, The Review of Financial
Studies, 19 (2006), 909-965.
[3] F. Black, M. Scholes, The
pricing of options and corporate liabilities, Journal of Political Economy,
81 (1973), 637-659.
[4] P. Capelli, F. Mariani, M.C.
Recchioni, F. Spinelli, F.Zirilli, Determining a stable relationship between
hedge fund index HFRI-Equity and S&P 500 behaviour, using filtering and maximum
likelihood,Inverse Problems in Science and Engineering 18 (2010),83-109.
[5] L.Fatone,
F. Mariani, M.C.Recchioni, F.Zirilli, Maximum likelihood estimation of the
parameters of a system of stochastic differential equations that models the returns
of the index of some classes of hedge funds, Journal of Inverse and
Ill-Posed Problems, 15 (2007), 329-362, http://www.econ.univpm.it/recchioni/finance/w5.
[6] L. Fatone, F. Mariani, M.C. Recchioni,
F.Zirilli, The calibration of the Heston stochastic volatility model using
filtering and maximum likelihood methods, in Proceedings of Dynamic Systems and Applications,
G.S.Ladde, N.G.Medhin, Chuang Peng, M.Sambandham Editors, Dynamic Publishers, Atlanta, USA, 5 (2008), 170-181, http://www.econ.univpm.it/recchioni/finance/w6.
[7] A. Harvey, R. Whaley, Market volatility prediction and the efficiency of the S&P 500
Index Option Market, Journal of Financial Economics, 31 (1992), 43-74.
[8] S.L. Heston, A closed-form solution for
options with stochastic volatility with applications to bond and currency
options, The Review of Financial Studies, 6 (1993), 327-343.
[9] F. Mariani, G.
Pacelli, F. Zirilli, Maximum likelihood
estimation of the Heston stochastic volatility model using asset and option
prices: an application of nonlinear filtering theory, Optimization Letters, 2 (2008), 177-222, http://www.econ.univpm.it/pacelli/mariani/w1.
[10] P. Pillonel, L. Solanet, Predictability
in hedge fund index returns and its application in fund of hedge funds style
allocation, Master's Thesis in Banking and Finance at Université de
Lausanne, Hautes Etudes Commerciales (HEC), 2006. (downloadable from the website:
http://www.hec.unil.ch/cms_mbf/master_thesis/0403.pdf).
TABLE 1: Historical data
|
i |
date |
variation HFRI
Equity Hedge Index |
variation S&P
500 |
HFRI Equity
Hedge Index |
S&P
500
|
HFRI Equity Hedge return |
S&P 500 return |
|
0 |
31/12/1989 |
-- |
-- |
--- |
--- |
0.00000 |
0.00000 |
|
1 |
31/01/1990 |
-3.34% |
-6.88% |
-3.340E-02 |
-6.880E-02 |
-0.03397 |
-0.07128 |
|
2 |
28/02/1990 |
2.85% |
0.85% |
2.850E-02 |
8.539E-03 |
-0.00587 |
-0.06278 |
|
3 |
31/03/1990 |
5.67% |
2.43% |
5.670E-02 |
2.426E-02 |
0.04928 |
-0.03881 |
|
4 |
30/04/1990 |
-0.87% |
-2.69% |
-8.700E-03 |
-2.689E-02 |
0.04054 |
-0.06607 |
|
5 |
31/05/1990 |
5.92% |
9.20% |
5.920E-02 |
9.199E-02 |
0.09806 |
0.02194 |
|
6 |
30/06/1990 |
2.52% |
-0.89% |
2.520E-02 |
-8.886E-03 |
0.12295 |
0.01301 |
|
7 |
31/07/1990 |
2.00% |
-0.52% |
2.000E-02 |
-5.223E-03 |
0.14275 |
0.00777 |
|
8 |
31/08/1990 |
-1.88% |
-9.43% |
-1.880E-02 |
-9.431E-02 |
0.12377 |
-0.09129 |
|
9 |
30/09/1990 |
1.65% |
-5.12% |
1.650E-02 |
-5.118E-02 |
0.14013 |
-0.14382 |
|
10 |
31/10/1990 |
0.77% |
-0.67% |
7.700E-03 |
-6.698E-03 |
0.14780 |
-0.15054 |
|
11 |
30/11/1990 |
-2.29% |
5.99% |
-2.290E-02 |
5.993E-02 |
0.12464 |
-0.09234 |
|
12 |
31/12/1990 |
1.02% |
2.48% |
1.020E-02 |
2.483E-02 |
0.13479 |
-0.06781 |
|
13 |
31/01/1991 |
4.90% |
4.15% |
4.900E-02 |
4.152E-02 |
0.18262 |
-0.02713 |
|
14 |
28/02/1991 |
5.20% |
6.73% |
5.200E-02 |
6.728E-02 |
0.23332 |
0.03798 |
|
15 |
31/03/1991 |
7.22% |
2.22% |
7.220E-02 |
2.220E-02 |
0.30303 |
0.05994 |
|
16 |
30/04/1991 |
0.47% |
0.03% |
4.700E-03 |
3.198E-04 |
0.30772 |
0.06026 |
|
17 |
31/05/1991 |
3.20% |
3.86% |
3.200E-02 |
3.860E-02 |
0.33922 |
0.09813 |
|
18 |
30/06/1991 |
0.59% |
-4.79% |
5.900E-03 |
-4.789E-02 |
0.34510 |
0.04906 |
|
19 |
31/07/1991 |
1.41% |
4.49% |
1.410E-02 |
4.486E-02 |
0.35910 |
0.09294 |
|
20 |
31/08/1991 |
2.17% |
1.96% |
2.170E-02 |
1.965E-02 |
0.38057 |
0.11240 |
|
21 |
30/09/1991 |
4.30% |
-1.91% |
4.300E-02 |
-1.914E-02 |
0.42267 |
0.09308 |
|
22 |
31/10/1991 |
1.16% |
1.18% |
1.160E-02 |
1.183E-02 |
0.43420 |
0.10484 |
|
23 |
30/11/1991 |
-1.08% |
-4.39% |
-1.080E-02 |
-4.390E-02 |
0.42335 |
0.05994 |
|
24 |
31/12/1991 |
5.02% |
11.16% |
5.020E-02 |
1.116E-01 |
0.47233 |
0.16574 |
|
25 |
31/01/1992 |
2.49% |
-1.99% |
2.490E-02 |
-1.990E-02 |
0.49692 |
0.14564 |
|
26 |
29/02/1992 |
2.90% |
0.96% |
2.900E-02 |
9.565E-03 |
0.52551 |
0.15516 |
|
27 |
31/03/1992 |
-0.28% |
-2.18% |
-2.800E-03 |
-2.183E-02 |
0.52270 |
0.13309 |
|
28 |
30/04/1992 |
0.27% |
2.79% |
2.700E-03 |
2.789E-02 |
0.52540 |
0.16060 |
|
29 |
31/05/1992 |
0.85% |
0.10% |
8.500E-03 |
9.640E-04 |
0.53386 |
0.16156 |
|
30 |
30/06/1992 |
-0.92% |
-1.74% |
-9.200E-03 |
-1.736E-02 |
0.52462 |
0.14405 |
|
31 |
31/07/1992 |
2.76% |
3.94% |
2.760E-02 |
3.940E-02 |
0.55185 |
0.18269 |
|
32 |
31/08/1992 |
-0.85% |
-2.40% |
-8.500E-03 |
-2.402E-02 |
0.54331 |
0.15838 |
|
33 |
30/09/1992 |
2.51% |
0.91% |
2.510E-02 |
9.106E-03 |
0.56810 |
0.16744 |
|
34 |
31/10/1992 |
2.03% |
0.21% |
2.030E-02 |
2.106E-03 |
0.58820 |
0.16955 |
|
35 |
30/11/1992 |
4.51% |
3.03% |
4.510E-02 |
3.026E-02 |
0.63231 |
0.19936 |
|
36 |
31/12/1992 |
3.38% |
1.01% |
3.380E-02 |
1.011E-02 |
0.66555 |
0.20942 |
|
37 |
31/01/1993 |
2.09% |
0.70% |
2.090E-02 |
7.046E-03 |
0.68624 |
0.21644 |
|
38 |
28/02/1993 |
-0.57% |
1.05% |
-5.700E-03 |
1.048E-02 |
0.68052 |
0.22687 |
|
39 |
31/03/1993 |
3.26% |
1.87% |
3.260E-02 |
1.870E-02 |
0.71260 |
0.24539 |
|
40 |
30/04/1993 |
1.30% |
-2.54% |
1.300E-02 |
-2.542E-02 |
0.72552 |
0.21964 |
|
41 |
31/05/1993 |
2.72% |
2.27% |
2.720E-02 |
2.272E-02 |
0.75235 |
0.24211 |
|
42 |
30/06/1993 |
3.01% |
0.08% |
3.010E-02 |
7.552E-04 |
0.78201 |
0.24287 |
|
43 |
31/07/1993 |
2.12% |
-0.53% |
2.120E-02 |
-5.327E-03 |
0.80299 |
0.23752 |
|
44 |
31/08/1993 |
3.84% |
3.44% |
3.840E-02 |
3.443E-02 |
0.84067 |
0.27137 |
|
45 |
30/09/1993 |
2.52% |
-1.00% |
2.520E-02 |
-9.988E-03 |
0.86556 |
0.26134 |
|
46 |
31/10/1993 |
3.11% |
1.94% |
3.110E-02 |
1.939E-02 |
0.89618 |
0.28054 |
|
47 |
30/11/1993 |
-1.93% |
-1.29% |
-1.930E-02 |
-1.291E-02 |
0.87669 |
0.26755 |
|
48 |
31/12/1993 |
3.59% |
1.01% |
3.590E-02 |
1.009E-02 |
0.91197 |
0.27759 |
|
49 |
31/01/1994 |
2.35% |
3.25% |
2.350E-02 |
3.250E-02 |
0.93519 |
0.30957 |
|
50 |
28/02/1994 |
-0.40% |
-3.00% |
-4.000E-03 |
-3.005E-02 |
0.93119 |
0.27906 |
|
51 |
31/03/1994 |
-2.08% |
-4.57% |
-2.080E-02 |
-4.575E-02 |
0.91017 |
0.23223 |
|
52 |
30/04/1994 |
-0.37% |
1.15% |
-3.700E-03 |
1.153E-02 |
0.90646 |
0.24369 |
|
53 |
31/05/1994 |
0.41% |
1.24% |
4.100E-03 |
1.242E-02 |
0.91055 |
0.25604 |
|
54 |
30/06/1994 |
-0.41% |
-2.68% |
-4.100E-03 |
-2.681E-02 |
0.90644 |
0.22886 |
|
55 |
31/07/1994 |
0.91% |
3.15% |
9.100E-03 |
3.149E-02 |
0.91550 |
0.25986 |
|
56 |
31/08/1994 |
1.27% |
3.76% |
1.270E-02 |
3.762E-02 |
0.92812 |
0.29679 |
|
57 |
30/09/1994 |
1.32% |
-2.69% |
1.320E-02 |
-2.690E-02 |
0.94123 |
0.26953 |
|
58 |
31/10/1994 |
0.40% |
2.08% |
4.000E-03 |
2.083E-02 |
0.94523 |
0.29014 |
|
59 |
30/11/1994 |
-1.48% |
-3.95% |
-1.480E-02 |
-3.950E-02 |
0.93032 |
0.24984 |
|
60 |
31/12/1994 |
0.74% |
1.23% |
7.400E-03 |
1.230E-02 |
0.93769 |
0.26207 |
|
61 |
31/01/1995 |
0.30% |
2.43% |
3.000E-03 |
2.428E-02 |
0.94068 |
0.28606 |
|
62 |
28/02/1995 |
1.68% |
3.61% |
1.680E-02 |
3.607E-02 |
0.95734 |
0.32149 |
|
63 |
31/03/1995 |
2.09% |
2.73% |
2.090E-02 |
2.733E-02 |
0.97803 |
0.34845 |
|
64 |
30/04/1995 |
2.64% |
2.80% |
2.640E-02 |
2.796E-02 |
1.00409 |
0.37603 |
|
65 |
31/05/1995 |
1.22% |
3.63% |
1.220E-02 |
3.631E-02 |
1.01621 |
0.41170 |
|
66 |
30/06/1995 |
4.73% |
2.13% |
4.730E-02 |
2.128E-02 |
1.06243 |
0.43275 |
|
67 |
31/07/1995 |
4.46% |
3.18% |
4.460E-02 |
3.178E-02 |
1.10606 |
0.46404 |
|
68 |
31/08/1995 |
2.93% |
-0.03% |
2.930E-02 |
-3.203E-04 |
1.13494 |
0.46372 |
|
69 |
30/09/1995 |
2.90% |
4.01% |
2.900E-02 |
4.010E-02 |
1.16353 |
0.50303 |
|
70 |
31/10/1995 |
-1.44% |
-0.50% |
-1.440E-02 |
-4.979E-03 |
1.14902 |
0.49804 |
|
71 |
30/11/1995 |
3.43% |
4.10% |
3.430E-02 |
4.105E-02 |
1.18275 |
0.53827 |
|
72 |
31/12/1995 |
2.56% |
1.74% |
2.560E-02 |
1.744E-02 |
1.20803 |
0.55556 |
|
73 |
31/01/1996 |
1.06% |
3.26% |
1.060E-02 |
3.262E-02 |
1.21857 |
0.58766 |
|
74 |
29/02/1996 |
2.82% |
0.69% |
2.820E-02 |
6.934E-03 |
1.24638 |
0.59457 |
|
75 |
31/03/1996 |
1.90% |
0.79% |
1.900E-02 |
7.917E-03 |
1.26520 |
0.60246 |
|
76 |
30/04/1996 |
5.34% |
1.34% |
5.340E-02 |
1.343E-02 |
1.31723 |
0.61580 |
|
77 |
31/05/1996 |
3.70% |
2.29% |
3.700E-02 |
2.285E-02 |
1.35356 |
0.63839 |
|
78 |
30/06/1996 |
-0.73% |
0.23% |
-7.300E-03 |
2.257E-03 |
1.34623 |
0.64065 |
|
79 |
31/07/1996 |
-2.87% |
-4.57% |
-2.870E-02 |
-4.575E-02 |
1.31711 |
0.59382 |
|
80 |
31/08/1996 |
2.63% |
1.88% |
2.630E-02 |
1.881E-02 |
1.34307 |
0.61245 |
|
81 |
30/09/1996 |
2.18% |
5.42% |
2.180E-02 |
5.417E-02 |
1.36464 |
0.66521 |
|
82 |
31/10/1996 |
1.56% |
2.61% |
1.560E-02 |
2.613E-02 |
1.38012 |
0.69100 |
|
83 |
30/11/1996 |
1.66% |
7.34% |
1.660E-02 |
7.338E-02 |
1.39658 |
0.76181 |
|
84 |
31/12/1996 |
0.83% |
-2.15% |
8.300E-03 |
-2.151E-02 |
1.40485 |
0.74007 |
|
85 |
31/01/1997 |
2.78% |
6.13% |
2.780E-02 |
6.132E-02 |
1.43227 |
0.79958 |
|
86 |
28/02/1997 |
-0.24% |
0.59% |
-2.400E-03 |
5.928E-03 |
1.42986 |
0.80549 |
|
87 |
31/03/1997 |
-0.73% |
-4.26% |
-7.300E-03 |
-4.261E-02 |
1.42254 |
0.76195 |
|
88 |
30/04/1997 |
-0.27% |
5.84% |
-2.700E-03 |
5.841E-02 |
1.41983 |
0.81871 |
|
89 |
31/05/1997 |
5.04% |
5.86% |
5.040E-02 |
5.858E-02 |
1.46900 |
0.87564 |
|
90 |
30/06/1997 |
1.97% |
4.35% |
1.970E-02 |
4.345E-02 |
1.48851 |
0.91818 |
|
91 |
31/07/1997 |
5.05% |
7.81% |
5.050E-02 |
7.812E-02 |
1.53778 |
0.99339 |
|
92 |
31/08/1997 |
1.35% |
-5.74% |
1.350E-02 |
-5.745E-02 |
1.55119 |
0.93423 |
|
93 |
30/09/1997 |
5.69% |
5.32% |
5.690E-02 |
5.315E-02 |
1.60653 |
0.98601 |
|
94 |
31/10/1997 |
0.39% |
-3.45% |
3.900E-03 |
-3.448E-02 |
1.61042 |
0.95093 |
|
95 |
30/11/1997 |
-0.93% |
4.46% |
-9.300E-03 |
4.459E-02 |
1.60108 |
0.99455 |
|
96 |
31/12/1997 |
1.42% |
1.57% |
1.420E-02 |
1.573E-02 |
1.61518 |
1.01016 |
|
97 |
31/01/1998 |
-0.16% |
1.02% |
-1.600E-03 |
1.015E-02 |
1.61358 |
1.02026 |
|
98 |
28/02/1998 |
4.09% |
7.04% |
4.090E-02 |
7.045E-02 |
1.65366 |
1.08834 |
|
99 |
31/03/1998 |
4.54% |
4.99% |
4.540E-02 |
4.995E-02 |
1.69806 |
1.13708 |
|
100 |
30/04/1998 |
1.39% |
0.91% |
1.390E-02 |
9.076E-03 |
1.71187 |
1.14611 |
|
101 |
31/05/1998 |
-1.27% |
-1.88% |
-1.270E-02 |
-1.883E-02 |
1.69908 |
1.12710 |
|
102 |
30/06/1998 |
0.50% |
3.94% |
5.000E-03 |
3.944E-02 |
1.70407 |
1.16579 |
|
103 |
31/07/1998 |
-0.67% |
-1.16% |
-6.700E-03 |
-1.162E-02 |
1.69735 |
1.15410 |
|
104 |
31/08/1998 |
-7.65% |
-14.58% |
-7.650E-02 |
-1.458E-01 |
1.61777 |
0.99651 |
|
105 |
30/09/1998 |
3.16% |
6.24% |
3.160E-02 |
6.240E-02 |
1.64888 |
1.05704 |
|
106 |
31/10/1998 |
2.47% |
8.03% |
2.470E-02 |
8.029E-02 |
1.67328 |
1.13427 |
|
107 |
30/11/1998 |
3.84% |
5.91% |
3.840E-02 |
5.913E-02 |
1.71096 |
1.19172 |
|
108 |
31/12/1998 |
5.39% |
5.64% |
5.390E-02 |
5.638E-02 |
1.76345 |
1.24656 |
|
109 |
31/01/1999 |
4.98% |
4.10% |
4.980E-02 |
4.101E-02 |
1.81205 |
1.28675 |
|
110 |
28/02/1999 |
-2.41% |
-3.23% |
-2.410E-02 |
-3.228E-02 |
1.78766 |
1.25394 |
|
111 |
31/03/1999 |
4.05% |
3.88% |
4.050E-02 |
3.879E-02 |
1.82736 |
1.29200 |
|
112 |
30/04/1999 |
5.25% |
3.79% |
5.250E-02 |
3.794E-02 |
1.87853 |
1.32924 |
|
113 |
31/05/1999 |
1.22% |
-2.50% |
1.220E-02 |
-2.497E-02 |
1.89066 |
1.30395 |
|
114 |
30/06/1999 |
3.80% |
5.44% |
3.800E-02 |
5.444E-02 |
1.92795 |
1.35696 |
|
115 |
31/07/1999 |
0.61% |
-3.20% |
6.100E-03 |
-3.205E-02 |
1.93403 |
1.32438 |
|
116 |
31/08/1999 |
0.04% |
-0.63% |
4.000E-04 |
-6.254E-03 |
1.93443 |
1.31811 |
|
117 |
30/09/1999 |
0.35% |
-2.86% |
3.500E-03 |
-2.855E-02 |
1.93793 |
1.28915 |
|
118 |
31/10/1999 |
2.33% |
6.25% |
2.330E-02 |
6.254E-02 |
1.96096 |
1.34981 |
|
119 |
30/11/1999 |
6.76% |
1.91% |
6.760E-02 |
1.906E-02 |
2.02637 |
1.36869 |
|
120 |
31/12/1999 |
10.88% |
5.78% |
1.088E-01 |
5.784E-02 |
2.12965 |
1.42492 |
|
121 |
31/01/2000 |
0.25% |
-5.09% |
2.500E-03 |
-5.090E-02 |
2.13215 |
1.37268 |
|
122 |
29/02/2000 |
10.00% |
-2.01% |
1.000E-01 |
-2.011E-02 |
2.22746 |
1.35236 |
|
123 |
31/03/2000 |
1.73% |
9.67% |
1.730E-02 |
9.672E-02 |
2.24461 |
1.44469 |
|
124 |
30/04/2000 |
-4.19% |
-3.08% |
-4.190E-02 |
-3.080E-02 |
2.20181 |
1.41340 |
|
125 |
31/05/2000 |
-2.44% |
-2.19% |
-2.440E-02 |
-2.191E-02 |
2.17710 |
1.39125 |
|
126 |
30/06/2000 |
4.85% |
2.39% |
4.850E-02 |
2.393E-02 |
2.22446 |
1.41490 |
|
127 |
31/07/2000 |
-1.58% |
-1.63% |
-1.580E-02 |
-1.634E-02 |
2.20854 |
1.39842 |
|
128 |
31/08/2000 |
5.35% |
6.07% |
5.350E-02 |
6.070E-02 |
2.26066 |
1.45735 |
|
129 |
30/09/2000 |
-1.08% |
-5.35% |
-1.080E-02 |
-5.348E-02 |
2.24980 |
1.40239 |
|
130 |
31/10/2000 |
-2.01% |
-0.49% |
-2.010E-02 |
-4.949E-03 |
2.22949 |
1.39743 |
|
131 |
30/11/2000 |
-4.30% |
-8.01% |
-4.300E-02 |
-8.007E-02 |
2.18554 |
1.31397 |
|
132 |
31/12/2000 |
3.16% |
0.41% |
3.160E-02 |
4.053E-03 |
2.21665 |
1.31801 |
|
133 |
31/01/2001 |
2.88% |
3.46% |
2.880E-02 |
3.464E-02 |
2.24504 |
1.35207 |
|
134 |
28/02/2001 |
-2.56% |
-9.23% |
-2.560E-02 |
-9.229E-02 |
2.21911 |
1.25524 |
|
135 |
31/03/2001 |
-2.30% |
-6.42% |
-2.300E-02 |
-6.420E-02 |
2.19584 |
1.18888 |
|
136 |
30/04/2001 |
2.27% |
7.68% |
2.270E-02 |
7.681E-02 |
2.21829 |
1.26289 |
|
137 |
31/05/2001 |
0.90% |
0.51% |
9.000E-03 |
5.090E-03 |
2.22725 |
1.26796 |
|
138 |
30/06/2001 |
-0.32% |
-2.50% |
-3.200E-03 |
-2.500E-02 |
2.22404 |
1.24264 |
|
139 |
31/07/2001 |
-1.06% |
-1.08% |
-1.060E-02 |
-1.077E-02 |
2.21339 |
1.23182 |
|
140 |
31/08/2001 |
-1.22% |
-6.41% |
-1.220E-02 |
-6.411E-02 |
2.20111 |
1.16556 |
|
141 |
30/09/2001 |
-3.73% |
-8.17% |
-3.730E-02 |
-8.172E-02 |
2.16310 |
1.08031 |
|
142 |
31/10/2001 |
1.85% |
1.81% |
1.850E-02 |
1.810E-02 |
2.18143 |
1.09824 |
|
143 |
30/11/2001 |
1.97% |
7.52% |
1.970E-02 |
7.518E-02 |
2.20094 |
1.17073 |
|
144 |
31/12/2001 |
1.99% |
0.76% |
1.990E-02 |
7.574E-03 |
2.22064 |
1.17828 |
|
145 |
31/01/2002 |
0.22% |
-1.56% |
2.200E-03 |
-1.557E-02 |
2.22284 |
1.16258 |
|
146 |
28/02/2002 |
-0.89% |
-2.08% |
-8.900E-03 |
-2.077E-02 |
2.21390 |
1.14160 |
|
147 |
31/03/2002 |
2.03% |
3.67% |
2.030E-02 |
3.674E-02 |
2.23400 |
1.17768 |
|
148 |
30/04/2002 |
0.17% |
-6.14% |
1.700E-03 |
-6.142E-02 |
2.23570 |
1.11429 |
|
149 |
31/05/2002 |
0.00% |
-0.91% |
0.000E+00 |
-9.081E-03 |
2.23570 |
1.10517 |
|
150 |
30/06/2002 |
-2.63% |
-7.25% |
-2.630E-02 |
-7.246E-02 |
2.20904 |
1.02995 |
|
151 |
31/07/2002 |
-3.93% |
-7.90% |
-3.930E-02 |
-7.900E-02 |
2.16895 |
0.94765 |
|
152 |
31/08/2002 |
0.28% |
0.49% |
2.800E-03 |
4.881E-03 |
2.17175 |
0.95252 |
|
153 |
30/09/2002 |
-1.96% |
-11.00% |
-1.960E-02 |
-1.100E-01 |
2.15195 |
0.83599 |
|
154 |
31/10/2002 |
0.56% |
8.64% |
5.600E-03 |
8.645E-02 |
2.15754 |
0.91890 |
|
155 |
30/11/2002 |
2.67% |
5.71% |
2.670E-02 |
5.707E-02 |
2.18389 |
0.97440 |
|
156 |
31/12/2002 |
-1.14% |
-6.03% |
-1.140E-02 |
-6.033E-02 |
2.17242 |
0.91218 |
|
157 |
31/01/2003 |
-0.01% |
-2.74% |
-1.000E-04 |
-2.741E-02 |
2.17232 |
0.88439 |
|
158 |
28/02/2003 |
-0.78% |
-1.70% |
-7.800E-03 |
-1.700E-02 |
2.16449 |
0.86724 |
|
159 |
31/03/2003 |
-0.07% |
0.84% |
-7.000E-04 |
8.358E-03 |
2.16379 |
0.87556 |
|
160 |
30/04/2003 |
2.43% |
8.10% |
2.430E-02 |
8.104E-02 |
2.18780 |
0.95349 |
|
161 |
31/05/2003 |
4.08% |
5.09% |
4.080E-02 |
5.090E-02 |
2.22779 |
1.00313 |
|
162 |
30/06/2003 |
1.52% |
1.13% |
1.520E-02 |
1.132E-02 |
2.24287 |
1.01439 |
|
163 |
31/07/2003 |
2.41% |
1.62% |
2.410E-02 |
1.622E-02 |
2.26669 |
1.03048 |
|
164 |
31/08/2003 |
2.38% |
1.79% |
2.380E-02 |
1.787E-02 |
2.29021 |
1.04819 |
|
165 |
30/09/2003 |
0.78% |
-1.19% |
7.800E-03 |
-1.194E-02 |
2.29798 |
1.03618 |
|
166 |
31/10/2003 |
3.12% |
5.50% |
3.120E-02 |
5.496E-02 |
2.32870 |
1.08968 |
|
167 |
30/11/2003 |
1.14% |
0.71% |
1.140E-02 |
7.129E-03 |
2.34004 |
1.09679 |
|
168 |
31/12/2003 |
1.93% |
5.08% |
1.930E-02 |
5.077E-02 |
2.35915 |
1.14631 |
|
169 |
31/01/2004 |
1.95% |
1.73% |
1.950E-02 |
1.728E-02 |
2.37847 |
1.16344 |
|
170 |
29/02/2004 |
1.11% |
1.22% |
1.110E-02 |
1.221E-02 |
2.38951 |
1.17558 |
|
171 |
31/03/2004 |
0.36% |
-1.64% |
3.600E-03 |
-1.636E-02 |
2.39310 |
1.15908 |
|
172 |
30/04/2004 |
-2.08% |
-1.68% |
-2.080E-02 |
-1.679E-02 |
2.37208 |
1.14215 |
|
173 |
31/05/2004 |
-0.19% |
1.21% |
-1.900E-03 |
1.208E-02 |
2.37018 |
1.15416 |
|
174 |
30/06/2004 |
1.07% |
1.80% |
1.070E-02 |
1.799E-02 |
2.38082 |
1.17199 |
|
175 |
31/07/2004 |
-1.88% |
-3.43% |
-1.880E-02 |
-3.429E-02 |
2.36184 |
1.13710 |
|
176 |
31/08/2004 |
-0.37% |
0.23% |
-3.700E-03 |
2.287E-03 |
2.35814 |
1.13938 |
|
177 |
30/09/2004 |
1.99% |
0.94% |
1.990E-02 |
9.364E-03 |
2.37784 |
1.14870 |
|
178 |
31/10/2004 |
0.48% |
1.40% |
4.800E-03 |
1.401E-02 |
2.38263 |
1.16261 |
|
179 |
30/11/2004 |
3.37% |
3.86% |
3.370E-02 |
3.859E-02 |
2.41577 |
1.20048 |
|
180 |
31/12/2004 |
1.76% |
3.25% |
1.760E-02 |
3.246E-02 |
2.43322 |
1.23242 |
|
181 |
31/01/2005 |
-0.58% |
-2.53% |
-5.800E-03 |
-2.529E-02 |
2.42740 |
1.20681 |
|
182 |
28/02/2005 |
2.13% |
1.89% |
2.130E-02 |
1.890E-02 |
2.44848 |
1.22553 |
|
183 |
31/03/2005 |
-1.05% |
-1.91% |
-1.050E-02 |
-1.912E-02 |
2.43792 |
1.20623 |
|
184 |
30/04/2005 |
-2.23% |
-2.01% |
-2.230E-02 |
-2.011E-02 |
2.41537 |
1.18591 |
|
185 |
31/05/2005 |
1.55% |
3.00% |
1.550E-02 |
2.995E-02 |
2.43075 |
1.21542 |
|
186 |
30/06/2005 |
1.96% |
-0.01% |
1.960E-02 |
-1.427E-04 |
2.45016 |
1.21528 |
|
187 |
31/07/2005 |
2.95% |
3.60% |
2.950E-02 |
3.597E-02 |
2.47924 |
1.25062 |
|
188 |
31/08/2005 |
0.74% |
-1.12% |
7.400E-03 |
-1.122E-02 |
2.48661 |
1.23933 |
|
189 |
30/09/2005 |
2.25% |
0.69% |
2.250E-02 |
6.949E-03 |
2.50886 |
1.24626 |
|
190 |
31/10/2005 |
-1.87% |
-1.77% |
-1.870E-02 |
-1.774E-02 |
2.48998 |
1.22836 |
|
191 |
30/11/2005 |
2.14% |
3.52% |
2.140E-02 |
3.519E-02 |
2.51116 |
1.26294 |
|
192 |
31/12/2005 |
2.32% |
-0.10% |
2.320E-02 |
-9.524E-04 |
2.53409 |
1.26199 |
|
193 |
31/01/2006 |
3.95% |
2.55% |
3.950E-02 |
2.547E-02 |
2.57283 |
1.28714 |
|
194 |
28/02/2006 |
0.02% |
0.05% |
2.000E-04 |
4.531E-04 |
2.57303 |
1.28759 |
|
195 |
31/03/2006 |
2.55% |
1.11% |
2.550E-02 |
1.106E-02 |
2.59821 |
1.29859 |
|
196 |
30/04/2006 |
1.76% |
1.22% |
1.760E-02 |
1.219E-02 |
2.61566 |
1.31071 |
|
197 |
31/05/2006 |
-2.32% |
-3.09% |
-2.320E-02 |
-3.092E-02 |
2.59219 |
1.27930 |
|
198 |
30/06/2006 |
-0.54% |
0.01% |
-5.400E-03 |
8.661E-05 |
2.58677 |
1.27939 |
|
199 |
31/07/2006 |
-0.54% |
0.51% |
-5.400E-03 |
5.086E-03 |
2.58136 |
1.28446 |
|
200 |
31/08/2006 |
1.03% |
2.13% |
1.030E-02 |
2.127E-02 |
2.59160 |
1.30551 |
|
201 |
30/09/2006 |
0.16% |
2.46% |
1.600E-03 |
2.457E-02 |
2.59320 |
1.32978 |
|
202 |
31/10/2006 |
1.86% |
3.15% |
1.860E-02 |
3.151E-02 |
2.61163 |
1.36081 |
|
203 |
30/11/2006 |
2.00% |
1.65% |
2.000E-02 |
1.647E-02 |
2.63143 |
1.37714 |
|
204 |
31/12/2006 |
1.35% |
1.26% |
1.350E-02 |
1.262E-02 |
2.64484 |
1.38968 |
|
205 |
31/01/2007 |
1.16% |
1.41% |
1.160E-02 |
1.406E-02 |
2.65638 |
1.40364 |
|
206 |
28/02/2007 |
0.63% |
-2.18% |
6.300E-03 |
-2.185E-02 |
2.66266 |
1.38155 |
|
207 |
31/03/2007 |
1.02% |
1.00% |
1.020E-02 |
9.980E-03 |
2.67281 |
1.39148 |
|
208 |
30/04/2007 |
1.95% |
4.33% |
1.950E-02 |
4.329E-02 |
2.69212 |
1.43386 |
|
209 |
31/05/2007 |
2.29% |
3.25% |
2.290E-02 |
3.255E-02 |
2.71476 |
1.46589 |
|
210 |
30/06/2007 |
1.09% |
-1.78% |
1.090E-02 |
-1.782E-02 |
2.72560 |
1.44791 |
TABLE 3: Forecasted values of the log-returns
|
i |
date |
one month variation (in per cent) of the S&P 500
index
|
one month variation (in per cent) of the HFRI Equity hedge fund index
|
observed one month return
|
forecasted
one month return |
observed six months return
|
forecasted
six months return |
|
1 |
31/01/1990 |
-6.88% |
-3.34% |
|
|
|
|
|
2 |
28/02/1990 |
0.85% |
2.85% |
|
|
|
|
|
3 |
31/03/1990 |
2.43% |
5.67% |
|
|
|
|
|
4 |
30/04/1990 |
-2.69% |
-0.87% |
|
|
|
|
|
5 |
31/05/1990 |
9.20% |
5.92% |
|
|
|
|
|
6 |
30/06/1990 |
-0.89% |
2.52% |
2.52E-02 |
6.55E-03 |
|
|
|
7 |
31/07/1990 |
-0.52% |
2.00% |
2.00E-02 |
1.18E-02 |
|
|
|
8 |
31/08/1990 |
-9.43% |
-1.88% |
-1.88E-02 |
1.10E-02 |
|
|
|
9 |
30/09/1990 |
-5.12% |
1.65% |
1.65E-02 |
4.48E-03 |
|
|
|
10 |
31/10/1990 |
-0.67% |
0.77% |
7.70E-03 |
6.66E-03 |
|
|
|
11 |
30/11/1990 |
5.99% |
-2.29% |
-2.29E-02 |
2.33E-03 |
2.694E-02 |
3.993E-02 |
|
12 |
31/12/1990 |
2.48% |
1.02% |
1.02E-02 |
1.63E-03 |
1.191E-02 |
7.308E-02 |
|
13 |
31/01/1991 |
4.15% |
4.90% |
4.90E-02 |
-2.97E-03 |
4.068E-02 |
6.786E-02 |
|
14 |
28/02/1991 |
6.73% |
5.20% |
5.20E-02 |
3.42E-03 |
1.158E-01 |
2.717E-02 |
|
15 |
31/03/1991 |
2.22% |
7.22% |
7.22E-02 |
6.43E-03 |
1.769E-01 |
4.062E-02 |
|
16 |
30/04/1991 |
0.03% |
0.47% |
4.70E-03 |
2.00E-02 |
1.734E-01 |
1.409E-02 |
|
17 |
31/05/1991 |
3.86% |
3.20% |
3.20E-02 |
1.53E-02 |
2.393E-01 |
9.814E-03 |
|
18 |
30/06/1991 |
-4.79% |
0.59% |
5.90E-03 |
1.64E-02 |
2.341E-01 |
-1.766E-02 |
|
19 |
31/07/1991 |
4.49% |
1.41% |
1.41E-02 |
2.28E-02 |
1.930E-01 |
2.071E-02 |
|
20 |
31/08/1991 |
1.96% |
2.17% |
2.17E-02 |
5.36E-03 |
1.586E-01 |
3.921E-02 |
|
21 |
30/09/1991 |
-1.91% |
4.30% |
4.30E-02 |
6.54E-03 |
1.271E-01 |
1.262E-01 |
|
22 |
31/10/1991 |
1.18% |
1.16% |
1.16E-02 |
1.34E-02 |
1.348E-01 |
9.517E-02 |
|
23 |
30/11/1991 |
-4.39% |
-1.08% |
-1.08E-02 |
1.18E-02 |
8.777E-02 |
1.026E-01 |
|
24 |
31/12/1991 |
11.16% |
5.02% |
5.02E-02 |
1.00E-02 |
1.357E-01 |
1.445E-01 |
|
25 |
31/01/1992 |
-1.99% |
2.49% |
2.49E-02 |
1.48E-02 |
1.478E-01 |
3.261E-02 |
|
26 |
29/02/1992 |
0.96% |
2.90% |
2.90E-02 |
1.72E-02 |
1.560E-01 |
3.990E-02 |
|
27 |
31/03/1992 |
-2.18% |
-0.28% |
-2.80E-03 |
1.35E-02 |
1.052E-01 |
8.335E-02 |
|
28 |
30/04/1992 |
2.79% |
0.27% |
2.70E-03 |
1.06E-02 |
9.548E-02 |
7.318E-02 |
|
29 |
31/05/1992 |
0.10% |
0.85% |
8.50E-03 |
1.59E-02 |
1.169E-01 |
6.176E-02 |
|
30 |
30/06/1992 |
-1.74% |
-0.92% |
-9.20E-03 |
8.66E-03 |
5.369E-02 |
9.231E-02 |
|
31 |
31/07/1992 |
3.94% |
2.76% |
2.76E-02 |
4.94E-03 |
5.646E-02 |
1.079E-01 |
|
32 |
31/08/1992 |
-2.40% |
-0.85% |
-8.50E-03 |
4.88E-03 |
1.796E-02 |
8.346E-02 |
|
33 |
30/09/1992 |
0.91% |
2.51% |
2.51E-02 |
4.50E-03 |
4.644E-02 |
6.531E-02 |
|
34 |
31/10/1992 |
0.21% |
2.03% |
2.03E-02 |
4.80E-03 |
6.481E-02 |
9.928E-02 |
|
35 |
30/11/1992 |
3.03% |
4.51% |
4.51E-02 |
4.37E-03 |
1.035E-01 |
5.308E-02 |
|
36 |
31/12/1992 |
1.01% |
3.38% |
3.38E-02 |
1.22E-02 |
1.513E-01 |
3.001E-02 |
|
37 |
31/01/1993 |
0.70% |
2.09% |
2.09E-02 |
1.30E-02 |
1.438E-01 |
2.966E-02 |
|
38 |
28/02/1993 |
1.05% |
-0.57% |
-5.70E-03 |
1.90E-02 |
1.471E-01 |
2.731E-02 |
|
39 |
31/03/1993 |
1.87% |
3.26% |
3.26E-02 |
1.22E-02 |
1.555E-01 |
2.913E-02 |
|
40 |
30/04/1993 |
-2.54% |
1.30% |
1.30E-02 |
1.62E-02 |
1.472E-01 |
2.654E-02 |
|
41 |
31/05/1993 |
2.27% |
2.72% |
2.72E-02 |
1.18E-02 |
1.275E-01 |
7.539E-02 |
|
42 |
30/06/1993 |
0.08% |
3.01% |
3.01E-02 |
1.04E-02 |
1.235E-01 |
8.066E-02 |
|
43 |
31/07/1993 |
-0.53% |
2.12% |
2.12E-02 |
1.36E-02 |
1.238E-01 |
1.195E-01 |
|
44 |
31/08/1993 |
3.44% |
3.84% |
3.84E-02 |
1.54E-02 |
1.737E-01 |
7.566E-02 |
|
45 |
30/09/1993 |
-1.00% |
2.52% |
2.52E-02 |
1.75E-02 |
1.653E-01 |
1.015E-01 |
|
46 |
31/10/1993 |
1.94% |
3.11% |
3.11E-02 |
1.84E-02 |
1.861E-01 |
7.300E-02 |
|
47 |
30/11/1993 |
-1.29% |
-1.93% |
-1.93E-02 |
1.91E-02 |
1.324E-01 |
6.430E-02 |
|
48 |
31/12/1993 |
1.01% |
3.59% |
3.59E-02 |
1.23E-02 |
1.388E-01 |
8.470E-02 |
|
49 |
31/01/1994 |
3.25% |
2.35% |
2.35E-02 |
1.28E-02 |
1.413E-01 |
9.576E-02 |
|
50 |
28/02/1994 |
-3.00% |
-0.40% |
-4.00E-03 |
1.20E-02 |
9.474E-02 |
1.095E-01 |
|
51 |
31/03/1994 |
-4.57% |
-2.08% |
-2.08E-02 |
7.95E-03 |
4.562E-02 |
1.158E-01 |
|
52 |
30/04/1994 |
1.15% |
-0.37% |
-3.70E-03 |
4.35E-03 |
1.033E-02 |
1.202E-01 |
|
53 |
31/05/1994 |
1.24% |
0.41% |
4.10E-03 |
3.93E-03 |
3.444E-02 |
7.632E-02 |
|
54 |
30/06/1994 |
-2.68% |
-0.41% |
-4.10E-03 |
-1.39E-03 |
-5.508E-03 |
7.920E-02 |
|
55 |
31/07/1994 |
3.15% |
0.91% |
9.10E-03 |
-5.35E-03 |
-1.950E-02 |
7.448E-02 |
|
56 |
31/08/1994 |
3.76% |
1.27% |
1.27E-02 |
-3.47E-03 |
-3.059E-03 |
4.868E-02 |
|
57 |
30/09/1994 |
-2.69% |
1.32% |
1.32E-02 |
4.48E-03 |
3.156E-02 |
2.639E-02 |
|
58 |
31/10/1994 |
2.08% |
0.40% |
4.00E-03 |
4.21E-03 |
3.953E-02 |
2.381E-02 |
|
59 |
30/11/1994 |
-3.95% |
-1.48% |
-1.48E-02 |
2.82E-03 |
1.996E-02 |
-8.331E-03 |
|
60 |
31/12/1994 |
1.23% |
0.74% |
7.40E-03 |
2.45E-03 |
3.174E-02 |
-3.169E-02 |
|
61 |
31/01/1995 |
2.43% |
0.30% |
3.00E-03 |
2.54E-03 |
2.550E-02 |
-2.064E-02 |
|
62 |
28/02/1995 |
3.61% |
1.68% |
1.68E-02 |
4.04E-03 |
2.965E-02 |
2.718E-02 |
|
63 |
31/03/1995 |
2.73% |
2.09% |
2.09E-02 |
2.54E-03 |
3.748E-02 |
2.555E-02 |
|
64 |
30/04/1995 |
2.80% |
2.64% |
2.64E-02 |
4.70E-03 |
6.063E-02 |
1.705E-02 |
|
65 |
31/05/1995 |
3.63% |
1.22% |
1.22E-02 |
9.33E-03 |
8.969E-02 |
1.477E-02 |
|
66 |
30/06/1995 |
2.13% |
4.73% |
4.73E-02 |
9.14E-03 |
1.329E-01 |
1.536E-02 |
|
67 |
31/07/1995 |
3.18% |
4.46% |
4.46E-02 |
1.59E-02 |
1.798E-01 |
2.448E-02 |
|
68 |
31/08/1995 |
-0.03% |
2.93% |
2.93E-02 |
1.89E-02 |
1.943E-01 |
1.535E-02 |
|
69 |
30/09/1995 |
4.01% |
2.90% |
2.90E-02 |
2.14E-02 |
2.038E-01 |
2.852E-02 |
|
70 |
31/10/1995 |
-0.50% |
-1.44% |
-1.44E-02 |
1.92E-02 |
1.560E-01 |
5.730E-02 |
|
71 |
30/11/1995 |
4.10% |
3.43% |
3.43E-02 |
1.72E-02 |
1.812E-01 |
5.608E-02 |
|
72 |
31/12/1995 |
1.74% |
2.56% |
2.56E-02 |
1.57E-02 |
1.567E-01 |
9.919E-02 |
|
73 |
31/01/1996 |
3.26% |
1.06% |
1.06E-02 |
1.32E-02 |
1.191E-01 |
1.188E-01 |
|
74 |
29/02/1996 |
0.69% |
2.82% |
2.82E-02 |
1.06E-02 |
1.179E-01 |
1.352E-01 |
|
75 |
31/03/1996 |
0.79% |
1.90% |
1.90E-02 |
1.07E-02 |
1.070E-01 |
1.211E-01 |
|
76 |
30/04/1996 |
1.34% |
5.34% |
5.34E-02 |
1.56E-02 |
1.832E-01 |
1.078E-01 |
|
77 |
31/05/1996 |
2.29% |
3.70% |
3.70E-02 |
1.85E-02 |
1.863E-01 |
9.766E-02 |
|
78 |
30/06/1996 |
0.23% |
-0.73% |
-7.30E-03 |
2.00E-02 |
1.482E-01 |
8.200E-02 |
|
79 |
31/07/1996 |
-4.57% |
-2.87% |
-2.87E-02 |
1.66E-02 |
1.036E-01 |
6.507E-02 |
|
80 |
31/08/1996 |
1.88% |
2.63% |
2.63E-02 |
8.76E-03 |
1.015E-01 |
6.613E-02 |
|
81 |
30/09/1996 |
5.42% |
2.18% |
2.18E-02 |
9.14E-03 |
1.045E-01 |
9.762E-02 |
|
82 |
31/10/1996 |
2.61% |
1.56% |
1.56E-02 |
5.59E-03 |
6.491E-02 |
1.163E-01 |
|
83 |
30/11/1996 |
7.34% |
1.66% |
1.66E-02 |
4.54E-03 |
4.396E-02 |
1.263E-01 |
|
84 |
31/12/1996 |
-2.15% |
0.83% |
8.30E-03 |
6.47E-03 |
6.037E-02 |
1.038E-01 |
|
85 |
31/01/1997 |
6.13% |
2.78% |
2.78E-02 |
1.19E-02 |
1.220E-01 |
5.374E-02 |
|
86 |
28/02/1997 |
0.59% |
-0.24% |
-2.40E-03 |
1.14E-02 |
9.067E-02 |
5.610E-02 |
|
87 |
31/03/1997 |
-4.26% |
-0.73% |
-7.30E-03 |
8.02E-03 |
5.961E-02 |
3.398E-02 |
|
88 |
30/04/1997 |
5.84% |
-0.27% |
-2.70E-03 |
4.68E-03 |
4.052E-02 |
2.753E-02 |
|
89 |
31/05/1997 |
5.86% |
5.04% |
5.04E-02 |
4.58E-03 |
7.511E-02 |
3.942E-02 |
|
90 |
30/06/1997 |
4.35% |
1.97% |
1.97E-02 |
7.34E-03 |
8.727E-02 |
7.370E-02 |
|
91 |
31/07/1997 |
7.81% |
5.05% |
5.05E-02 |
6.88E-03 |
1.113E-01 |
7.040E-02 |
|
92 |
31/08/1997 |
-5.74% |
1.35% |
1.35E-02 |
1.40E-02 |
1.290E-01 |
4.910E-02 |
|
93 |
30/09/1997 |
5.32% |
5.69% |
5.69E-02 |
1.86E-02 |
2.020E-01 |
2.842E-02 |
|
94 |
31/10/1997 |
-3.45% |
0.39% |
3.90E-03 |
2.43E-02 |
2.100E-01 |
2.779E-02 |
|
95 |
30/11/1997 |
4.46% |
-0.93% |
-9.30E-03 |
1.84E-02 |
1.412E-01 |
4.482E-02 |
|
96 |
31/12/1997 |
1.57% |
1.42% |
1.42E-02 |
9.80E-03 |
1.350E-01 |
4.199E-02 |
|
97 |
31/01/1998 |
1.02% |
-0.16% |
-1.60E-03 |
6.82E-03 |
7.874E-02 |
8.665E-02 |
|
98 |
28/02/1998 |
7.04% |
4.09% |
4.09E-02 |
6.72E-03 |
1.079E-01 |
1.172E-01 |
|
99 |
31/03/1998 |
4.99% |
4.54% |
4.54E-02 |
4.78E-03 |
9.585E-02 |
1.551E-01 |
|
100 |
30/04/1998 |
0.91% |
1.39% |
1.39E-02 |
9.83E-03 |
1.068E-01 |
1.154E-01 |
|
101 |
31/05/1998 |
-1.88% |
-1.27% |
-1.27E-02 |
1.26E-02 |
1.030E-01 |
6.026E-02 |
|
102 |
30/06/1998 |
3.94% |
0.50% |
5.00E-03 |
1.06E-02 |
9.297E-02 |
4.161E-02 |
|
103 |
31/07/1998 |
-1.16% |
-0.67% |
-6.70E-03 |
1.10E-02 |
8.738E-02 |
4.100E-02 |
|
104 |
31/08/1998 |
-14.58% |
-7.65% |
-7.65E-02 |
4.39E-03 |
-3.526E-02 |
2.904E-02 |
|
105 |
30/09/1998 |
6.24% |
3.16% |
3.16E-02 |
-8.70E-03 |
-4.800E-02 |
6.042E-02 |
|
106 |
31/10/1998 |
8.03% |
2.47% |
2.47E-02 |
-9.49E-03 |
-3.785E-02 |
7.819E-02 |
|
107 |
30/11/1998 |
5.91% |
3.84% |
3.84E-02 |
-4.50E-03 |
1.194E-02 |
6.498E-02 |
|
108 |
31/12/1998 |
5.64% |
5.39% |
5.39E-02 |
4.29E-03 |
6.118E-02 |
6.790E-02 |
|
109 |
31/01/1999 |
4.10% |
4.98% |
4.98E-02 |
5.03E-03 |
1.215E-01 |
2.662E-02 |
|
110 |
28/02/1999 |
-3.23% |
-2.41% |
-2.41E-02 |
2.63E-02 |
1.852E-01 |
-5.108E-02 |
|
111 |
31/03/1999 |
3.88% |
4.05% |
4.05E-02 |
1.56E-02 |
1.954E-01 |
-5.558E-02 |
|
112 |
30/04/1999 |
3.79% |
5.25% |
5.25E-02 |
1.37E-02 |
2.278E-01 |
-2.667E-02 |
|
113 |
31/05/1999 |
-2.50% |
1.22% |
1.22E-02 |
1.95E-02 |
1.969E-01 |
2.602E-02 |
|
114 |
30/06/1999 |
5.44% |
3.80% |
3.80E-02 |
2.72E-02 |
1.788E-01 |
3.055E-02 |
|
115 |
31/07/1999 |
-3.20% |
0.61% |
6.10E-03 |
1.60E-02 |
1.297E-01 |
1.686E-01 |
|
116 |
31/08/1999 |
-0.63% |
0.04% |
4.00E-04 |
1.99E-02 |
1.581E-01 |
9.733E-02 |
|
117 |
30/09/1999 |
-2.86% |
0.35% |
3.50E-03 |
1.55E-02 |
1.169E-01 |
8.488E-02 |
|
118 |
31/10/1999 |
6.25% |
2.33% |
2.33E-02 |
7.13E-03 |
8.592E-02 |
1.228E-01 |
|
119 |
30/11/1999 |
1.91% |
6.76% |
6.76E-02 |
7.55E-03 |
1.454E-01 |
1.746E-01 |
|
120 |
31/12/1999 |
5.78% |
10.88% |
1.09E-01 |
1.56E-02 |
2.235E-01 |
9.959E-02 |
|
121 |
31/01/2000 |
-5.09% |
0.25% |
2.50E-03 |
2.53E-02 |
2.191E-01 |
1.253E-01 |
|
122 |
29/02/2000 |
-2.01% |
10.00% |
1.00E-01 |
2.19E-02 |
3.405E-01 |
9.659E-02 |
|
123 |
31/03/2000 |
9.67% |
1.73% |
1.73E-02 |
3.03E-02 |
3.589E-01 |
4.357E-02 |
|
124 |
30/04/2000 |
-3.08% |
-4.19% |
-4.19E-02 |
3.70E-02 |
2.723E-01 |
4.614E-02 |
|
125 |
31/05/2000 |
-2.19% |
-2.44% |
-2.44E-02 |
2.26E-02 |
1.627E-01 |
9.711E-02 |
|
126 |
30/06/2000 |
2.39% |
4.85% |
4.85E-02 |
5.99E-03 |
9.945E-02 |
1.614E-01 |
|
127 |
31/07/2000 |
-1.63% |
-1.58% |
-1.58E-02 |
1.24E-02 |
7.938E-02 |
1.391E-01 |
|
128 |
31/08/2000 |
6.07% |
5.35% |
5.35E-02 |
-3.54E-03 |
3.376E-02 |
1.964E-01 |
|
129 |
30/09/2000 |
-5.35% |
-1.08% |
-1.08E-02 |
4.74E-03 |
5.201E-03 |
2.432E-01 |
|
130 |
31/10/2000 |
-0.49% |
-2.01% |
-2.01E-02 |
6.00E-03 |
2.807E-02 |
1.436E-01 |
|
131 |
30/11/2000 |
-8.01% |
-4.30% |
-4.30E-02 |
5.76E-03 |
8.473E-03 |
3.648E-02 |
|
132 |
31/12/2000 |
0.41% |
3.16% |
3.16E-02 |
-7.03E-03 |
-7.782E-03 |
7.690E-02 |
|
133 |
31/01/2001 |
3.46% |
2.88% |
2.88E-02 |
4.59E-03 |
3.718E-02 |
-2.107E-02 |
|
134 |
28/02/2001 |
-9.23% |
-2.56% |
-2.56E-02 |
-3.07E-03 |
-4.069E-02 |
2.877E-02 |
|
135 |
31/03/2001 |
-6.42% |
-2.30% |
-2.30E-02 |
-6.21E-03 |
-5.252E-02 |
3.656E-02 |
|
136 |
30/04/2001 |
7.68% |
2.27% |
2.27E-02 |
-6.29E-03 |
-1.114E-02 |
3.509E-02 |
|
137 |
31/05/2001 |
0.51% |
0.90% |
9.00E-03 |
4.25E-03 |
4.259E-02 |
-4.145E-02 |
|
138 |
30/06/2001 |
-2.50% |
-0.32% |
-3.20E-03 |
4.23E-03 |
7.419E-03 |
2.786E-02 |
|
139 |
31/07/2001 |
-1.08% |
-1.06% |
-1.06E-02 |
-4.85E-03 |
-3.116E-02 |
-1.829E-02 |
|
140 |
31/08/2001 |
-6.41% |
-1.22% |
-1.22E-02 |
-2.40E-03 |
-1.784E-02 |
-3.670E-02 |
|
141 |
30/09/2001 |
-8.17% |
-3.73% |
-3.73E-02 |
3.70E-03 |
-3.221E-02 |
-3.718E-02 |
|
142 |
31/10/2001 |
1.81% |
1.85% |
1.85E-02 |
-7.58E-03 |
-3.619E-02 |
2.577E-02 |
|
143 |
30/11/2001 |
7.52% |
1.97% |
1.97E-02 |
-7.25E-03 |
-2.597E-02 |
2.566E-02 |
|
144 |
31/12/2001 |
0.76% |
1.99% |
1.99E-02 |
-3.83E-03 |
-3.395E-03 |
-2.873E-02 |
|
145 |
31/01/2002 |
-1.56% |
0.22% |
2.20E-03 |
3.94E-03 |
9.498E-03 |
-1.429E-02 |
|
146 |
28/02/2002 |
-2.08% |
-0.89% |
-8.90E-03 |
3.89E-03 |
1.287E-02 |
2.241E-02 |
|
147 |
31/03/2002 |
3.67% |
2.03% |
2.03E-02 |
5.07E-03 |
7.347E-02 |
-4.462E-02 |
|
148 |
30/04/2002 |
-6.14% |
0.17% |
1.70E-03 |
5.29E-03 |
5.577E-02 |
-4.273E-02 |
|
149 |
31/05/2002 |
-0.91% |
0.00% |
-2.13E-18 |
3.90E-03 |
3.537E-02 |
-2.273E-02 |
|
150 |
30/06/2002 |
-7.25% |
-2.63% |
-2.63E-02 |
3.47E-03 |
-1.153E-02 |
2.390E-02 |
|
151 |
31/07/2002 |
-7.90% |
-3.93% |
-3.93E-02 |
-2.57E-03 |
-5.246E-02 |
2.360E-02 |
|
152 |
31/08/2002 |
0.49% |
0.28% |
2.80E-03 |
-7.13E-03 |
-4.128E-02 |
3.082E-02 |
|
153 |
30/09/2002 |
-11.00% |
-1.96% |
-1.96E-02 |
-9.70E-03 |
-7.877E-02 |
3.213E-02 |
|
154 |
31/10/2002 |
8.64% |
0.56% |
5.60E-03 |
-1.28E-02 |
-7.518E-02 |
2.366E-02 |
|
155 |
30/11/2002 |
5.71% |
2.67% |
2.67E-02 |
-1.10E-02 |
-5.049E-02 |
2.099E-02 |
|
156 |
31/12/2002 |
-6.03% |
-1.14% |
-1.14E-02 |
-5.42E-03 |
-3.596E-02 |
-1.532E-02 |
|
157 |
31/01/2003 |
-2.74% |
-0.01% |
-1.00E-04 |
3.66E-03 |
3.376E-03 |
-4.204E-02 |
|
158 |
28/02/2003 |
-1.70% |
-0.78% |
-7.80E-03 |
3.44E-03 |
-7.230E-03 |
-5.680E-02 |
|
159 |
31/03/2003 |
0.84% |
-0.07% |
-7.00E-04 |
3.95E-03 |
1.191E-02 |
-7.432E-02 |
|
160 |
30/04/2003 |
8.10% |
2.43% |
2.43E-02 |
3.83E-03 |
3.073E-02 |
-6.428E-02 |
|
161 |
31/05/2003 |
5.09% |
4.08% |
4.08E-02 |
3.65E-03 |
4.488E-02 |
-3.206E-02 |
|
162 |
30/06/2003 |
1.13% |
1.52% |
1.52E-02 |
5.84E-03 |
7.300E-02 |
2.218E-02 |
|
163 |
31/07/2003 |
1.62% |
2.41% |
2.41E-02 |
7.43E-03 |
9.896E-02 |
2.083E-02 |
|
164 |
31/08/2003 |
1.79% |
2.38% |
2.38E-02 |
1.29E-02 |
1.340E-01 |
2.393E-02 |
|
165 |
30/09/2003 |
-1.19% |
0.78% |
7.80E-03 |
1.81E-02 |
1.436E-01 |
2.322E-02 |
|
166 |
31/10/2003 |
5.50% |
3.12% |
3.12E-02 |
1.27E-02 |
1.513E-01 |
2.211E-02 |
|
167 |
30/11/2003 |
0.71% |
1.14% |
1.14E-02 |
1.06E-02 |
1.188E-01 |
3.554E-02 |
|
168 |
31/12/2003 |
5.08% |
1.93% |
1.93E-02 |
1.17E-02 |
1.233E-01 |
4.541E-02 |
|
169 |
31/01/2004 |
1.73% |
1.95% |
1.95E-02 |
1.13E-02 |
1.183E-01 |
8.010E-02 |
|
170 |
29/02/2004 |
1.22% |
1.11% |
1.11E-02 |
1.26E-02 |
1.044E-01 |
1.139E-01 |
|
171 |
31/03/2004 |
-1.64% |
0.36% |
3.60E-03 |
1.10E-02 |
9.979E-02 |
7.886E-02 |
|
172 |
30/04/2004 |
-1.68% |
-2.08% |
-2.08E-02 |
7.38E-03 |
4.433E-02 |
6.536E-02 |
|
173 |
31/05/2004 |
1.21% |
-0.19% |
-1.90E-03 |
3.97E-03 |
3.060E-02 |
7.245E-02 |
|
174 |
30/06/2004 |
1.80% |
1.07% |
1.07E-02 |
4.15E-03 |
2.190E-02 |
7.000E-02 |
|
175 |
31/07/2004 |
-3.43% |
-1.88% |
-1.88E-02 |
4.50E-03 |
-1.649E-02 |
7.810E-02 |
|
176 |
31/08/2004 |
0.23% |
-0.37% |
-3.70E-03 |
-5.65E-03 |
-3.088E-02 |
6.801E-02 |
|
177 |
30/09/2004 |
0.94% |
1.99% |
1.99E-02 |
-6.59E-03 |
-1.514E-02 |
4.512E-02 |
|
178 |
31/10/2004 |
1.40% |
0.48% |
4.80E-03 |
4.11E-03 |
1.060E-02 |
2.406E-02 |
|
179 |
30/11/2004 |
3.86% |
3.37% |
3.37E-02 |
4.19E-03 |
4.665E-02 |
2.517E-02 |
|
180 |
31/12/2004 |
3.25% |
1.76% |
1.76E-02 |
3.94E-03 |
5.380E-02 |
2.732E-02 |
|
181 |
31/01/2005 |
-2.53% |
-0.58% |
-5.80E-03 |
8.17E-03 |
6.776E-02 |
-3.344E-02 |
|
182 |
28/02/2005 |
1.89% |
2.13% |
2.13E-02 |
7.48E-03 |
9.455E-02 |
-3.890E-02 |
|
183 |
31/03/2005 |
-1.91% |
-1.05% |
-1.05E-02 |
8.24E-03 |
6.193E-02 |
2.492E-02 |
|
184 |
30/04/2005 |
-2.01% |
-2.23% |
-2.23E-02 |
6.12E-03 |
3.328E-02 |
2.541E-02 |
|
185 |
31/05/2005 |
3.00% |
1.55% |
1.55E-02 |
-1.73E-03 |
1.509E-02 |
2.387E-02 |
|
186 |
30/06/2005 |
-0.01% |
1.96% |
1.96E-02 |
-1.95E-03 |
1.709E-02 |
5.003E-02 |
|
187 |
31/07/2005 |
3.60% |
2.95% |
2.95E-02 |
4.32E-03 |
5.320E-02 |
4.572E-02 |
|
188 |
31/08/2005 |
-1.12% |
0.74% |
7.40E-03 |
4.73E-03 |
3.887E-02 |
5.045E-02 |
|
189 |
30/09/2005 |
0.69% |
2.25% |
2.25E-02 |
5.00E-03 |
7.351E-02 |
3.729E-02 |
|
190 |
31/10/2005 |
-1.77% |
-1.87% |
-1.87E-02 |
1.21E-02 |
7.746E-02 |
-1.036E-02 |
|
191 |
30/11/2005 |
3.52% |
2.14% |
2.14E-02 |
7.02E-03 |
8.373E-02 |
-1.164E-02 |
|
192 |
31/12/2005 |
-0.10% |
2.32% |
2.32E-02 |
7.29E-03 |
8.755E-02 |
2.618E-02 |
|
193 |
31/01/2006 |
2.55% |
3.95% |
3.95E-02 |
6.12E-03 |
9.812E-02 |
2.874E-02 |
|
194 |
28/02/2006 |
0.05% |
0.02% |
2.00E-04 |
1.13E-02 |
9.027E-02 |
3.036E-02 |
|
195 |
31/03/2006 |
1.11% |
2.55% |
2.55E-02 |
8.28E-03 |
9.347E-02 |
7.477E-02 |
|
196 |
30/04/2006 |
1.22% |
1.76% |
1.76E-02 |
1.38E-02 |
1.339E-01 |
4.286E-02 |
|
197 |
31/05/2006 |
-3.09% |
-2.32% |
-2.32E-02 |
1.38E-02 |
8.440E-02 |
4.455E-02 |
|
198 |
30/06/2006 |
0.01% |
-0.54% |
-5.40E-03 |
7.37E-03 |
5.409E-02 |
3.730E-02 |
|
199 |
31/07/2006 |
0.51% |
-0.54% |
-5.40E-03 |
4.48E-03 |
8.561E-03 |
7.002E-02 |
|
200 |
31/08/2006 |
2.13% |
1.03% |
1.03E-02 |
4.28E-03 |
1.875E-02 |
5.072E-02 |
|
201 |
30/09/2006 |
2.46% |
0.16% |
1.60E-03 |
-2.69E-03 |
-4.997E-03 |
8.591E-02 |
|
202 |
31/10/2006 |
3.15% |
1.86% |
1.86E-02 |
-4.46E-03 |
-4.019E-03 |
8.579E-02 |
|
203 |
30/11/2006 |
1.65% |
2.00% |
2.00E-02 |
4.77E-03 |
4.003E-02 |
4.502E-02 |
|
204 |
31/12/2006 |
1.26% |
1.35% |
1.35E-02 |
5.13E-03 |
5.979E-02 |
2.717E-02 |
|
205 |
31/01/2007 |
1.41% |
1.16% |
1.16E-02 |
7.51E-03 |
7.791E-02 |
2.596E-02 |
|
206 |
28/02/2007 |
-2.18% |
0.63% |
6.30E-03 |
7.69E-03 |
7.364E-02 |
-1.601E-02 |
|
207 |
31/03/2007 |
1.00% |
1.02% |
1.02E-02 |
8.54E-03 |
8.286E-02 |
-2.646E-02 |
|
208 |
30/04/2007 |
4.33% |
1.95% |
1.95E-02 |
7.41E-03 |
8.381E-02 |
2.896E-02 |
|
209 |
31/05/2007 |
3.25% |
2.29% |
2.29E-02 |
8.85E-03 |
8.690E-02 |
3.119E-02 |
|
210 |
30/06/2007 |
1.09% |
-1.76% |
-1.76E-02 |
8.85E-03 |
8.411E-02 |
4.589E-02 |