Furtivity and masking problems in time dependent electromagnetic obstacle scattering

Lorella Fatone
Dipartimento di Matematica Pura ed Applicata, Università di Modena e Reggio Emilia,
Via Campi 213/b, 41100 Modena, Italy
fatone.lorella@unimo.it
Maria Cristina Recchioni
Istituto di Teoria delle Decisioni e Finanza Innovativa (DE.F.IN.), Università di Ancona,
Piazza Martelli 8, 60121 Ancona, Italy
recchioni@posta.econ.unian.it
Francesco Zirilli
Dipartimento di Matematica ``G. Castelnuovo'', Università di Roma ``La Sapienza'',
Piazzale Aldo Moro 2, 00185 Roma, Italy
f.zirilli@caspur.it

Abstract

In this paper we consider furtivity and masking problems in time dependent three dimensional electromagnetic obstacle scattering. That is we propose a criterion based on a merit function to ``minimize" or to ``mask" the electromagnetic field scattered by a bounded obstacle when hit by an incoming electromagnetic field and with respect to this criterion we derive the optimal strategy. These problems are natural generalizations to the context of electromagnetic scattering of the furtivity problem in time dependent acoustic obstacle scattering presented in [1]. We propose mathematical models of the furtivity and masking time dependent three dimensional electromagnetic scattering problems that consist in optimal control problems for systems of partial differential equations derived from the Maxwell equations. These control problems are approached using the Pontryagin maximum principle. We formulate the first order optimality conditions for the control problems considered as exterior problems defined outside the obstacle for systems of partial differential equations. Moreover the first order optimality conditions derived are solved numerically with a highly parallelizable numerical method based on a perturbative series of the type considered in [2], [3]. Finally we assess and validate the mathematical models and the numerical method proposed analyzing the numerical results obtained with a parallel implementation of the numerical method in several experiments on test problems. Really impressive speed up factors are obtained executing the algorithms on a parallel machine when the number of processors used in the computation ranges between 1 and 100. Some virtual reality applications and some animations relative to the numerical experiments can be found in this website.

References

[1]: F. Mariani, M.C. Recchioni and F. Zirilli,``The use of the Pontryagin maximum principle in a furtivity problem in time-dependent acoustic obstacle scattering", Waves in Random Media, 11, 549-575 (2001).
[2]: E. Mecocci, L. Misici, M.C. Recchioni, and F. Zirilli, ``A new formalism for time dependent wave scattering from a bounded obstacle", Journal of the Acoustical Society of America, 107, 1825-1840 (2000).
[3]: M.C. Recchioni and F. Zirilli, ``A new formalism for time dependent electromagnetic scattering from a bounded obstacle", to appear in Journal of Engineering Mathematics (2003).

Warning: To see the virtual reality animations we reccomend to use at least the following resources:

- screen resolution: 1024 x 768
- video adapter: 8Mb
- processor: Pentium II or equivalent

We suggest the following VRML clients:

	Windows	Mac	UNIX/Linux
Cortona	X	X
Cosmo Player	X	X
OpenVRML (Under Developement)			X
FreeWRL (Under Developement)			X

Note that in a Unix/Linux environment the clients OpenVRML and FreeWRL allow the visualization of the virtual objects but not the visualization of the virtual scenes.

We propose two experiments involving the following two obstacles:

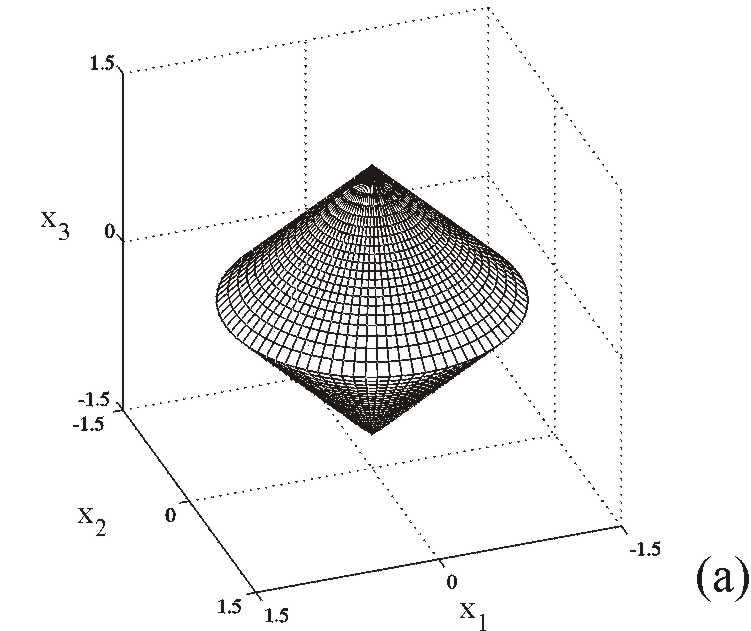Double Cone (virtual object): VRML visualization

Animation 1: Double Cone (gif file)

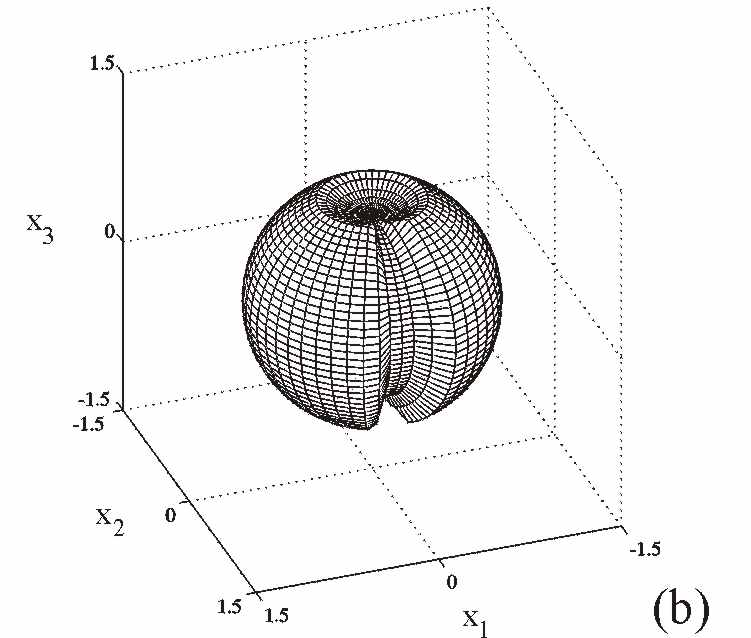Excavated Sphere (virtual object): VRML visualization

Animation 2: Excavated Sphere (virtual scene: VRML file)

Note that the electric field of the mask shown in the animation has been multiplied by a factor 5.

Acknowledgment: It is a pleasure to thank Mr. Adriano Tittarelli of Università di Ancona for the really helpful assistance in the realization of the virtual reality applications contained in this website.

Entry n.