Warning: To see the virtual reality animations we recommend to use at least the following resources:
- screen resolution: 1024 x 768 - video adapter: 8Mb - processor: Pentium II or equivalent
We suggest the following VRML clients:
| Windows | Mac | UNIX/Linux | |
| Cortona | X | X | |
| Cosmo Player | X | X | |
| OpenVRML (Under Developement) | X | ||
| FreeWRL (Under Developement) | X |
Note that in a Unix/Linux environment the clients OpenVRML and FreeWRL allow the visualization of virtual objects but not the visualization of virtual scenes.
Definite Band Furtivity Problem: Double Cone
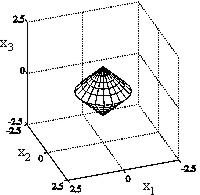 |
Double Cone (virtual object): VRML visualization |
Remark. In the following animations the time values shown in the twenty frames are t=-2+0.25j, j=0,1,...,19.
Definite Band Ghost Problem: Cube-Sphere
Remark.
In the following animations the scattered fields that is, the field
scattered by the passive obstacle, the field scattered by the active obstacle and the
field scattered by the ghost, are multiplied by 2. The time values shown in the twenty frames
of the animations are t=-3+0.75j,
j=0,1,...,19.
Furtivity effect outside the assigned frequency band
Data: incident wave ui=exp(-(z+t)2), band K=(-1, 1), scatterer double cone
Animation 2: Double Cone (gif file)
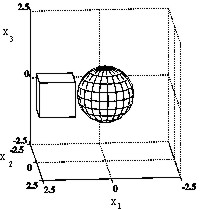
Cube-Sphere (virtual objects): VRML visualization
Ghost effect in the assigned frequency band:
Data: incident wave ui=exp(-(x-t)2), band K=(-∞, +∞), scatterer sphere, ghost cube
Animation 3: Cube-Sphere (Virtual scene: VRML file)
Ghost effect in the assigned frequency band:
The Animation 4 shows
on the surface of the sphere of center the origin and radius 3 the convolution of the inverse Fourier
transform of the characteristic function of the set K with the wave scattered by the passive obstacle,
with the wave scattered by active obstacle and with the wave scattered by the ghost respectively
in a colour
The x-axis
represents the spherical coordinate variable
f, 0£f
£2p and the y-axis represents the spherical coordinate
variable
q, 0£q
£p .
Data: incident wave ui=exp(-(x-t)2), band K=(-1.5, 1.5), scatterer sphere, ghost cube
Animation 4: Ghost Effect on the definite band K=(-1.5,1.5) (mpeg file)
Ghost effect outside the assigned frequency band:
The Animation 5 shows
on the surface of the sphere of center the origin and radius 3 the convolution of the inverse Fourier
transform of the characteristic function of the set IR\K with the wave scattered by the passive obstacle,
with the wave scattered by active obstacle and with the wave scattered by the ghost respectively
in a colour
The x-axis
represents the spherical coordinate variable
f, 0£f
£2p and the y-axis represents the spherical coordinate
variable
q, 0£q
£p .
Data: incident wave ui=exp(-(x-t)2), band K=(-1.5, 1.5), scatterer sphere, ghost cube
Animation 5: Ghost Effect outside of the definite band K=(-1.5,1.5) (mpeg file)