We present a highly parallelizable numerical
method to solve time dependent acoustic obstacle scattering
problems. The method proposed is a generalization of the
"operator expansion method" developed in [1]. Using a
Fourier transform with respect to time the time dependent
scattering problem for the wave equation considered
is transformed in an exterior boundary value problem
for the Helmholtz equation
depending on a parameter. The "operator
expansion method" is used to solve the
exterior problems for
the Helmholtz equation and reduces, via a perturbative approach,
the solution of each exterior problem to the solution of
a sequence of systems of first kind integral equations
defined on a suitable
"reference surface". The numerical solution of these systems of
integral equations is challenging when scattering problems
involving realistic obstacles and wavelengths small compared to
the characteristic dimensions of the obstacles are solved. Let
RT be the ratio between the characteristic dimension of the
obstacle and the wavelength considered. In the numerical
experiments presented the greater ratios RT considered
range in the interval [13,60]. This implies the use of
high dimensional vector spaces to approximate satisfactorily
the corresponding systems of integral equations.
That is each system of integral equations in the sequence mentioned above
after being
discretized to be solved numerically becomes a large system of
linear equations. Represented on a generic base the matrices that
approximate the integral operators after the discretization will
be dense matrices. We introduce a new way of using the wavelet
transform and new bases of wavelets and we develop a version
of the operator expansion method that constructs
directly element by element the coefficient matrix of the sparse
linear systems that
approximate in the wavelet basis considered the systems of
integral equations.
The resulting numerical method, using affordable computing resources,
is able to deal with
realistic acoustic scattering problems
solving large (sparse) linear systems
(up to approximately 5. 105 (real) unknowns and equations in the
numerical experience shown here). The computation of the elements
of the coefficient matrices of the linear systems considered and
several other aspects of the numerical algorithm proposed are
highly parallelizable allowing the development of an efficient
solver for exterior boundary value problems for the Helmholtz
equation. Several numerical experiments involving realistic
obstacles and "small" wavelengths are proposed. When possible the
quantitative character of the numerical results obtained
is established.
To evaluate the performance of the proposed algorithm on
parallel computing facilities appropriate speed
up factors are introduced and evaluated.
Some animations and virtual reality applications
relative to these numerical experiments can be found in this website.
Warning: To see the virtual reality applications
we recommend to use at least the following resources:
- screen resolution: 1024 x 768
- video adapter: 8Mb
- processor: Pentium II or equivalent
We suggest the following VRML clients:
| |
Windows |
Mac |
UNIX/Linux |
| Cortona |
X |
X |
|
| Cosmo Player |
X |
X |
|
| OpenVRML (Under Developement) |
|
|
X |
| FreeWRL (Under Developement) |
|
|
X |
Note that in a Unix/Linux environment the clients OpenVRML
and FreeWRL allow the visualization of virtual objects but not the
visualization of virtual scenes.
Time harmonic scattering from an acoustically soft sphere
Data: incident wave: ui=exp(-i(t-z)), c=1, radius of the sphere
r =1, RT=1/p
The following table shows the comparison between the approximate
solution obtained using the method proposed here and the approximate solution
obtained truncating at l=Lmax=10 the spherical harmonics expansion of the solution.
Time dependent scattering from a simplified version of a US Navy submarine
Remark.
In the following animations the time values shown in the twenty frames
are t=-70+(140/c)j/19, j=0,1,...,19, c=1532.8 meters/seconds.
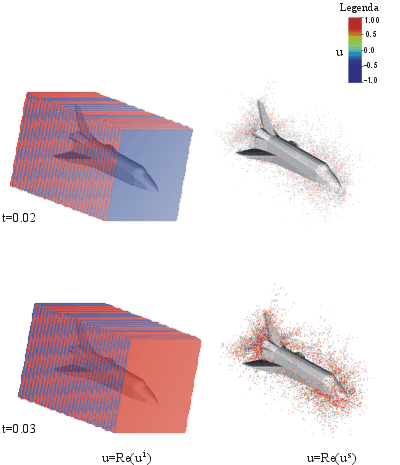
Time harmonic scattering from a simplified version of the NASA space shuttle
Remark.
In the following animations the time values shown in the twenty frames
are t=(2p/w) j/19, j=0,1,...,19,
w=(2p/3)c, c=331.45 meters/seconds
Time harmonic scattering from the simplified version of the Nasa space shuttle
Data: incident wave ui=exp(-i2p(z+ct)/3),
c=331.45 meters/seconds (sound speed in the air), length of the simplified version of the NASA space
shuttle L=56.14 meters,
RT=14/3
Animation 2: Click here to see the scattering phenomenon (Virtual scene: VRML file)
The following figure shows the time harmonic scattering from the simplified version
of Nasa space shuttle
when the incident wave is
ui=exp(-i8p(z+ct)) and c=331.45 meters/seconds,
this corresponds to RT=56.
Note that Re(*) means real part of the complex number * .
Entry n.





