 |
 |
A method to solve an acoustic inverse scattering problem involving smart obstacles
Lorella Fatone
Dipartimento di Matematica Pura ed Applicata
Università di Modena e Reggio Emilia
Via Campi 213/b, 41100 Modena, Italy
Ph. N. +39-059-2055589, FAX N. +39-059-370513
e-mail : fatone.lorella@unimo.it
Maria Cristina Recchioni
Dipartimento di Scienze Sociali "D. Serrani"
Università Politecnica delle Marche
Piazza Martelli 8, 60121 Ancona, Italy
Ph. N. +39-071-2207066, FAX N. +39-071-2207150
e-mail : m.c.recchioni@univpm.it
Francesco Zirilli
Dipartimento di Matematica "G. Castelnuovo"
Università di Roma "La Sapienza"
Piazzale Aldo Moro 2, 00185 Roma, Italy
Ph. N. +39-06-49913282, FAX N. +39-06-44701007
e-mail : f.zirilli@caspur.it
1. Abstract
A time harmonic acoustic inverse scattering problem involving smart obstacles is formulated and a method to solve it is proposed. A smart obstacle is an obstacle that when hit by an incoming acoustic wave tries to pursue a given goal circulating a suitable pressure current on its boundary. A pressure current is a quantity whose physical dimension is pressure divided by time. The goals pursued by the smart obstacles that we have considered are the following ones: to be undetectable or to appear with a shape and/or acoustic boundary impedance different from its actual ones eventually in a location in space different from the actual location. The following time harmonic inverse scattering problem is considered: from the knowledge of several far fields generated by the smart obstacle when hit by known time harmonic waves, the knowledge of the goal pursued by the smart obstacle and of its acoustic boundary impedance reconstruct the boundary of the obstacle. A method to solve this inverse problem that generalizes the so called Herglotz function method is proposed. Some numerical experiments that validate the method proposed are presented. This website contains some auxiliary material that helps the understanding of paper [10].
2. Introduction
The numerical experiment reported in Section 3 concerns a time harmonic acoustic inverse scattering problem involving a smart obstacle. Let IR3 be the three dimensional real Euclidean space, the obstacle considered is represented by a bounded simply connected open set W Ì IR3 with locally Lipschitz boundary ¶W having a non-negative constant boundary acoustic impedance c, immersed in a homogeneous non-viscous fluid, at rest in an equilibrium state, that fills IR3\W with no source terms present.
An usual obstacle, that here we call "passive" obstacle, when hit by an incoming time harmonic acoustic wave propagating in the medium generates a scattered field whose "knowledge" for sufficiently many incoming waves allows to recover an approximation of the main features of the obstacle such as its location, acoustic boundary impedance and shape.
The most usual time harmonic inverse scattering problem for a passive obstacle can be formulated as follows (see for example [1], [2], [3]):
Acoustic Time Harmonic Passive Inverse Scattering Problem: Given the knowledge of the far fields generated by the (passive) obstacle when hit by several known incoming time harmonic plane waves with different incident directions and/or different wave numbers and of the acoustic boundary impedance of the obstacle, determine the boundary of the obstacle.
We call "smart" obstacle an obstacle that when hit by an incoming wave takes actions to try to make difficult its identification. In fact a smart obstacle when hit by an incoming wave is able to pursue a goal, such as, for example, the goal of being undetectable [6], [7], or of being masked [5], [6] or of generating a ghost [4], that is the smart obstacle tries to scatter as little as possible, to appear with a shape and/or boundary impedance different from its actual ones or to appear outside a given region in space with a shape and/or boundary impedance in a location in space different from the actual ones respectively. The assigned goal is pursued circulating a suitable pressure current on the boundary ¶W of the smart obstacle. A pressure current is a quantity whose physical dimension is pressure divided by time. A mathematical model of the acoustic time harmonic direct scattering problems involving smart obstacles consists in a constrained optimization problem with the constraints given by an exterior boundary value problem for the Helmholtz equation (see [8] Section 2). The pressure current is the independent variable of the optimization problem.
In this website we show some numerical results concerning an inverse problem for a smart obstacle that tries to mask itself. We call this obstacle masked obstacle. This kind of smart obstacle pursues the goal of appearing with a shape and/or a boundary impedance different from its actual ones, that is when hit by an incoming wave it tries to make the field scattered by the obstacle W, with impedance c as similar as possible to the field scattered in the same circumstances by an obstacle WM with impedance cM. The obstacle (WM;cM) will be called mask. Note that the obstacle (WM;cM) is different from the obstacle (W;c) and that in the masking problem considered here the obstacle WM must be contained in the obstacle W. We assume that the mask (WM;cM) is a passive obstacle. Several numerical experiments concerning direct scattering problems involving smart obstacles can be found in the following websites:
The inverse problem corresponding to the direct time harmonic masking problem that we consider in this website
is the following:
Acoustic Time Harmonic Masking Inverse Scattering
Problem: From the knowledge
of several far fields generated by the masked obstacle when hit by known
incident acoustic waves when the optimal pressure current is active
and of the acoustic boundary impedances of the obstacle and
of the mask
find the shape of the obstacle. A similar inverse problem has been considered in [8].
Let us go into details in the description of the model.
Let IR, C be the sets of real and complex numbers respectively,
let
x = (x1,x2,x3)T Î IR3 be a generic
vector, where the superscript T means transposed, we denote with (·,·) the Euclidean scalar product in
IR3 and with ||·|| the corresponding Euclidean
vector norm.
We denote with
n(
x) = (n1(x),n2(x),n3(x))T Î IR3, x Î ¶W the outward unit normal vector to ¶W.
Since W has a locally Lipschitz boundary,
n(
x),
x Î ¶W, exists almost everywhere.
Finally we denote with cl(W)
the closure of
W. Remind that we assume that W is
characterized by a constant acoustic
boundary impedance c, such that c ³ 0 and that in the following we refer
to the couple (W;c) as the obstacle.
Note that the case of acoustically hard obstacles and/or acoustically hard masks, that is
obstacles and/or masks such that
c = +¥ and/or cM = +¥ can be treated with some
simple modifications of the formulae that follow.
Let us consider a passive obstacle (W;c) and an
acoustic incoming time harmonic plane wave whose spatial part is
given by:
where i Î C is the imaginary unit, c > 0 is the wave propagation velocity, w ¹ 0 is the frequency,
a Î IR3 is a unit vector and
k = w/c. The quantity
k = w/c is called wave number of the wave (1),
and the direction
a is the propagation direction of
the wave (1).
The passive obstacle (W;c) when hit by the time harmonic
incoming wave (1) generates a time harmonic scattered
field whose space dependent part usk,
a(
x) is the solution of the
following
boundary value problem for the
Helmholtz equation:
with the boundary condition:
and the Sommerfeld radiation condition at infinity:
where D = å3i = 1¶2/¶xi2 is the
Laplace operator, r = ||
x||,
x Î IR3 and o(·)
and later O(·) are the Landau symbols. The boundary value
problem (2)-(5) is the mathematical
formulation of the acoustic time harmonic direct (passive)
obstacle scattering problem.
Furthermore we recall that the following expansion of
the scattered field usk,
a solution of (2)-(5) holds:
where x = x/r, r ¹ 0. Expansion (6) says that when r® +¥ the leading term of the expansion in inverse powers
of r of usk, a is a spherical wave eik r /r
modulated by the so called "far field" F0,us.
Let usM,k,a(x), x
Î IR3\WM be the scattered field generated by the mask
(WM;cM) when hit by the incoming wave
(1), that is the solution of the boundary value problem
(2)-(5) when WM,
cM replace W, c respectively.
A mathematical model for the masking problem is given by an optimization problem (see [5]
for a precise formulation of this optimization problem) whose first order optimality
conditions are given by the following boundary value problem for two coupled
Helmholtz equations in the unknowns usk,
a(
x), fk,
a(x),
x Î IR3\W:
with the boundary conditions:
and the following conditions at infinity:
uik,
a(
x) = ei w(
x,
a)/c,
x Î IR3 , (1)
æ
è
D usk,
a+k2usk,
a
ö
ø
(
x) = 0,
x Î IR3\
cl
(W)
, (2)
ik usk,
a(
x) +c
¶ usk,
a
¶
n(
x)
(
x) = bk,
a(
x),
x Î ¶W, (3)
bk,
a(
x) = -i k ei k(
x,
a) (1+c(
n(
x),
a)),
x Î ¶W, (4)
¶usk,
a(
x)
¶ r
-i kusk,
a(
x) = o(
1
r
), r®+¥, (5)
usk,
a(
x) =
eik r
r
F0,us(
x
,k,
a)+O
æ
ç
è
1
r2
ö
÷
ø
, r® +¥ , (6)
æ
è
D usk,
a+k2 usk,
a
ö
ø
(x) = 0,
x Î IR3\ cl(
W)
, (7)
æ
è
D fk,
a+k2fk,
a
ö
ø
(x) = 0,
x Î IR3\
cl(
W)
, (8)
ik usk,
a(
x) +c
¶
usk,a
¶
n(
x)
(
x) +
(1+c)
V
fk,
a(
x) = bk,
a(
x),
x Î ¶W, (9)
(1-l) i k fk,
a(
x) -(1-l)c
¶ fk,
a
¶
n(
x)
(
x)+l(1+c) ( usk,
a(
x)- usM,k,
a(
x)) = 0,
x Î ¶W, (10)
¶usk,
a(
x)
¶ r
-i k usk,
a(
x) = o(
1
r
), r®+¥, (11)
¶ fk,
a(
x)
¶r
+i k fk,
a(
x) = o(
1
r
), r®+¥ , (12)
where 0 <l< 1 and V is a positive dimensional constant that we can choose equal to one without loss of generality. The parameters l, m=1-l, V appear in the objective function of the optimization problem that models the masking problem (see [5]).
Let usk, a( x), fk, a( x), x Î IR3\W be the solution of (7)-(12). The function fk, a( x), x Î IR3\W solution of (7)-(12) is an auxiliary function. The relation between this auxiliary function and the optimal pressure current y* is given by:
| (13) |
We note that the complex conjugate of the auxiliary function, fk, a, satisfies the Helmholtz equation (8) and the radiation condition at infinity (5), that is for the complex conjugate of fk, a the expansion (6) holds. That is in analogy with (6) the following expansion holds:
| (14) |
The inverse scattering problem considered consists in the reconstruction of the boundary of the smart obstacle ¶W from the knowledge of several far fields associated to the scattered acoustic field generated by the smart obstacle when hit by known time harmonic waves and from the knowledge of the goal pursued by the smart obstacle (i.e. being masked) and of the acoustic boundary impedances of the obstacle and of the mask. To solve this inverse problem we have developed a method that generalizes the so called Herglotz function method used for the solution of inverse obstacle scattering problems involving passive obstacles. The method is based on the definition of two Herglotz functions, one associated to the scattered acoustic field usk,a and one associated to the auxiliary function fk, a. Under some hypotheses the Herglotz functions are determined from the knowledge of the far fields associated to the acoustic scattered field. Once known the Herglotz functions we are able to determine the Herglotz wave functions and to reconstruct the boundary of the smart obstacle using ad hoc equations satisfied by the Herglotz wave functions on the boundary of the smart obstacle.
3. A Numerical Experiment
In the following Applet we show how the reconstruction of a smart obstacle
changes when we increase the number of far fields used in the reconstruction.
Let (r, q, n)
be the canonical spherical coordinate system.
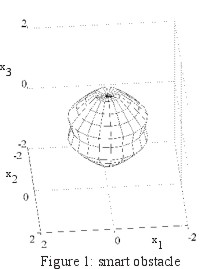
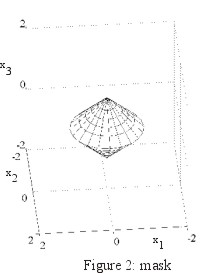
The setting of the numerical experiment consists in an acoustically soft (i.e. c=0) smart corrugated sphere
(i.e. the smart obstacle) (see Figure 1) that tries to appear as an acoustically soft
(i.e. cM=0) double cone (i.e. the mask) (see Figure 2). The smart corrugated
sphere is hit by an incoming plane wave
(1), that is:
| (15) |
where k=4, c=1,
a=(sinqcosn,
sinqsinn,cosq)T where
0 ≤ q ≤ p,
0 ≤ n < 2p, for some choices of the incoming direction
a.
 |
 |
That is we measure the far fields generated by the smart obstacle when hit by the incoming acoustic wave (1) when we choose a=aj =(0,sinqj,cosqj)T, qj=p(j-1)/8, j=1,2,...,9. Note that both the smart obstacle and the mask are cylindrically symmetric with respect to the x3-axis
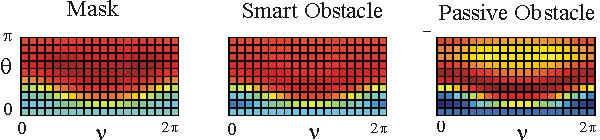
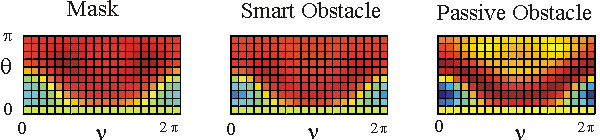
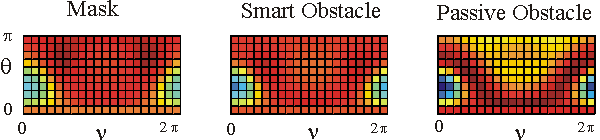
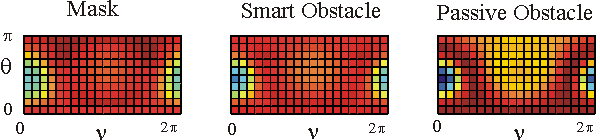
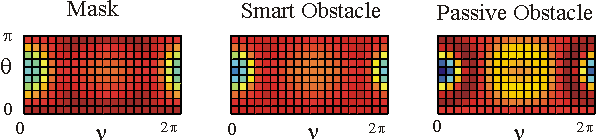
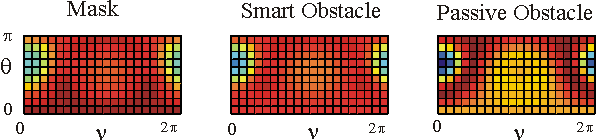
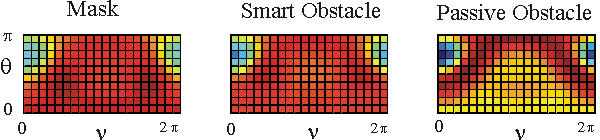
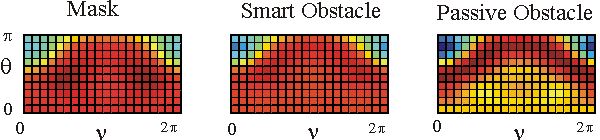
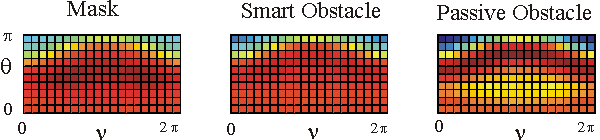
Table 1 shows in a colour the real part of the far fields associated to the acoustic scattered field generated by the mask, by the smart obstacle and by the passive obstacle respectively when the parameters defining the masking strategy have been chosen as follows: l=0.97, m=(1-l)=0.03, V=1. The images show that the far fields generated by the smart obstacle try to resemble to the corresponding far fields of the mask, that is they show the masking effect and that for some incoming propagation directions the masking effect is greater than for some other propagation directions. For example when we look to the far fields corresponding to q=q1 the masking effect is greater than when we look to the far fields corresponding to q=q4. Probably this is due to the large corrugation of the smart obstacle in the equatorial plane compared to the edge of the mask in the same plane.
The user can click on the individual images to see them in a bigger window.
The behaviour of the imaginary part of the far fields whose real part is shown in Table 1 is qualitatively similar to the behaviour of the real parts.
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
In the Applet of Section 4 we show nine frames one frame for each far field added to the data used to solve the inverse problem. Each frame contains four objects: far fields, mask, smart obstacle, reconstruction of the smart obstacle. The first object of the frames is made of nine images, these images are the real part of the far fields used to reconstruct the smart obstacle. The images relative to the far fields that are not used in the reconstruction shown in the current frame are blank. The last three objects in each frame are the images of the mask, of the smart obstacle and of the reconstruction of the smart obstacle obtained from the knowledge of the far fields shown. That is the first frame shows the reconstruction of the smart obstacle obtained using only the knowledge of the far field corresponding to the incident angle q1, the second frame shows the reconstruction obtained using two far fields corresponding to the incident angles q1,q2 and so on.
The images relative to the far fields contained in the frames of the Applet show in the q, n plane in a colour the real part of the far fields generated by the smart obstacle when hit by the incoming field given in (1) for a=aj =(0,sinqj, cosqj)T, j=1,2,...,9.
Finally we present a virtual reality animation of the numerical experiment discussed above to help the understanding of the behaviour of the reconstruction procedure. The virtual reality animation consists in four windows. Two windows are static windows showing the mask and the smart obstacle respectively. The remaining two windows are dynamic windows showing how the reconstruction of the smart obstacle varies when we increase from 1 to 9 the number of the far fields used as data. In particular one window shows the last far field added as datum and the other window shows the reconstruction of the smart obstacle obtained with the far fields used as data at that point. That is the far field shown in the other window and the far fields preceding it.
The real part of the last far field added as datum is represented in a colour on the surface of the unit sphere.
We note that each reconstruction shown in the applet and in the virtual animation requires an execution time less than ten minutes on a personal computer with Intel Pentium Centrino M 1.6GHz with 512MB DDR SDRAM.
4. Applet
The following Applet shows the results obtained in the numerical experiment described in the previous section. The user can see the effect on the reconstruction induced by the increasing number of far fields used as data. We remind that the user can move forward and backward in the vision of the images using the appropriate buttons.
5. References
6. Useful Links