A parallel numerical method to solve high frequency ghost obstacle acoustic scattering
problems*
Lorella Fatone
Dipartimento di Matematica Pura e Applicata,
Università di Modena e Reggio Emilia,
Via Campi 213/b, 41100 Modena, Italy
Ph. N. +39-059-2055589, FAX N. +39-059-370513,
E-mail: fatone.lorella@unimo.it
Maria Cristina Recchioni
Dipartimento di Scienze Sociali "D. Serrani",
Università Politecnica delle Marche,
Piazza Martelli 8, 60121 Ancona, Italy
Ph. N. +39-071-2207066, FAX N. +39-071-2207058,
E-mail: m.c.recchioni@univpm.it
Francesco Zirilli
Dipartimento di Matematica "G. Castelnuovo'', Università di
Roma "La Sapienza'',
Piazzale Aldo Moro 2, 00185 Roma, Italy
Ph. N. +39-06-49913282, FAX N. +39-06-44701007,
E-mail: f.zirilli@caspur.it
Abstract
A highly parallelizable numerical method for time dependent high
frequency acoustic scattering problems involving realistic smart
obstacles is proposed. A scatterer becomes smart when hit by an
incoming wave reacts circulating on its boundary a pressure
current to pursue a given goal. A pressure current is a quantity
whose physical dimension is pressure divided by time. In
particular we consider obstacles that when hit by an
incoming acoustic wave try to generate a virtual image of
themselves in a location in space different from their actual
location. The virtual image of the obstacle (i.e.: the ghost
obstacle) is seen outside a given set containing the obstacle and
its virtual image in the apparent location. We call this problem
ghost obstacle scattering problem.
We model this acoustic scattering
problem and several other acoustic scattering problems concerning
other types of smart
obstacles as optimal control problems for
the wave equation. Using the Pontryagin maximum principle the
first order optimality conditions associated to these control
problems are formulated. The numerical method proposed to solve
these optimality conditions is a variation of the operator
expansion method and reduces the solution of the optimal control
problem to the solution of a sequence of systems of integral
equations. These systems of integral equations are solved using
suitable wavelet bases to represent the unknowns, the data and the
integral kernels. These wavelet bases are made of piecewise
polynomial functions and have the property that the matrices that
represent the integral operators on these wavelet bases can be
approximated satisfactorily with very sparse matrices. This
property of the wavelet bases makes possible to approximate the
optimal control problems considered with linear systems of
equations with hundreds of thousands or millions of unknowns and
equations that can be stored and solved with affordable computing
resources, that is it makes possible to solve satisfactorily
problems with realistic obstacles hit by waves of small
wavelength. We validate the method proposed solving some test
problems, these problems are optimal control problems involving a
``smart" simplified version of the NASA space shuttle hit by
incoming waves with small wavelengths compared to its
characteristic dimension. We consider test problems with ratio
between the characteristic dimension of the obstacle and
the wavelength of the time harmonic component of the incoming wave up
to approximately sixty. The numerical results obtained are very
satisfactory. This website
contains stereoscopic and virtual reality applications showing
some numerical experiments relative to the problems studied in the paper associated to
the website. A more general reference to the work in acoustic and
electromagnetic scattering of the authors and of their coauthors
is the website:
http://www.econ.univpm.it/recchioni/scattering.
References
-
[1]
-
L.Fatone, G. Pacelli, M.C. Recchioni, F.Zirilli,
"Optimal control methods for two new classes of smart obstacles in
time dependent acoustic scattering", Journal of Engineering Mathematics, 56, 385--413
(2006).
-
[2]
-
F. Mariani, M.C. Recchioni and F. Zirilli, "The use of the Pontryagin
maximum principle in a furtivity problem in time-dependent acoustic obstacle
scattering", Waves in Random Media 11, 549-575 (2001).
-
[3]
-
L. Fatone, M. C. Recchioni and F. Zirilli,
"A masking
problem in time dependent acoustic obstacle scattering",
ARLO - {Acoustics Research Letters Online}, 5, Issue 2, 25-30 (2004).
-
[4]
- P. Corna, L. Fatone, M. C. Recchioni and
F. Zirilli, "Some mathematical models of
furtivity and masking problems in time dependent acoustic obstacle
scattering", in Mathematical Modelling of Wave Phenomena 2002,
Mathematical Modelling in Physics, Engineering and
Cognitive Sciences, edited by
B. Nilsson, L. Fishman, Vaxjo University Press, Vaxjo, Sweden, 7, 79-89, (2003).
-
[5]
- L. Fatone, M. C. Recchioni and F. Zirilli,
"Furtivity and masking problems in time dependent electromagnetic
obstacle scattering", Journal of Optimization Theory and Applications,
121, 223-257 (2004).
-
[6]
-
L. Fatone, M. C. Recchioni and F. Zirilli, "Mathematical
models of ``active" obstacles in acoustic scattering", in
Control and Boundary Analysis, edited by J. Cagnol and J. P.
Zolesio, Marcel Dekker/CRC Press, Boca Raton, Fl. USA, Lecture
Notes in Pure and Applied Mathematics 240, 2005, pp.
119--129.
-
[7]
-
L. Fatone, M. C. Recchioni and F. Zirilli, "A parallel numerical method to solve high frequency ghost
obstacle acoustic scattering problems", submitted to ACES journal
Acknowledgement
The numerical experience
reported in this paper has been obtained using the computing
resources of CASPUR (Roma, Italy) under grant: "Algoritmi di
alte prestazioni per problemi di scattering acustico". The support
and sponsorship of CASPUR are gratefully acknowledged.
It is a pleasure to thank Mr. Fabio Bonaccorso, Mr. Piero Lanucara
and Mrs. Claudia Truini of CASPUR (Roma, Italy) for the helpful assistance in the
realization of the stereoscopic applications contained in this website.
Warning: To see the (non stereoscopic) virtual reality applications
we recommend to use at least the following resources:
- screen resolution: 1024 x 768
- video adapter: 8Mb
- processor: Pentium II or equivalent
We suggest the following VRML clients:
| |
Windows |
Mac |
UNIX/Linux |
| Cortona |
X |
X |
|
| Cosmo Player |
X |
X |
|
| OpenVRML (Under Developement) |
|
|
X |
| FreeWRL (Under Developement) |
|
|
X |
To see the stereoscopic applications
click here and follow the instructions
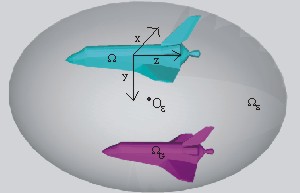
Time dependent scattering from a smart simplified version of the NASA space shuttle
Time dependent scattering from the smart simplified version of the Nasa space shuttle
Data: incident wave
ui=exp(-p2(a1x+a2y+a1z-ct)2),
where
a1=sin(p/4)cos(p/4),
a2=sin(p/4)sin(p/4),
a3=cos(p/4),
c=331.45 meters/seconds (sound speed in the air), the length of the simplified version of the NASA space
shuttle in the direction of its main body is L=56.14 meters. The z axis is the symmetry axis of the main body of the obstacle.
Let RT be the ratio between the characteristic dimension of the obstacle
and the wavelength of the time harmonic components of the incident wave considered.
The ratio RT in this experiment ranges approximately between 3 to 60. Remind that the incident wave
is approximated with a finite linear combination of time harmonic plane waves.
Animation 1: Click here to see the scattering phenomenon (Virtual scene: VRML file)
Remark.
In the animation the time values shown in twenty frames
are t=(-(j-1)(15/21)+7.5)/c, j=1,2,...,20,
c=331.45 meters/seconds
Entry n.