PAPER:
Wavelet bases made of piecewise polynomial functions: approximation theory, quadrature rules and applications to integral kernel sparsification
and image compression
*
Lorella Fatone
Dipartimento di Matematica e Informatica, Università di Camerino, Via Madonna delle Carceri 9, 62032 Camerino, Italy. Ph. N. +39-0737-402558, Fax N. +39-0737-632525, e-mail: lorella.fatone@unicam.it
Maria
Cristina Recchioni
Dipartimento di Scienze Sociali “D. Serrani”, Università Politecnica delle Marche, Piazza Martelli 8, 60121 Ancona, Italy. Ph. N. +39-071-2207066, Fax N. +39-071-2207150, e-mail: m.c.recchioni@univpm.it
Francesco Zirilli
Dipartimento di Matematica “G.
Castelnuovo”, Università di Roma “La Sapienza”,
Piazzale Aldo Moro 2, 00185 Roma, Italy. Ph. N. +39-06-49913282, Fax N.
+39-06-44701007, e-mail: f.zirilli@caspur.it
1.
Abstract
2.
Introduction
3.
Examples of MATLAB Symbolic
Math codes that compute the wavelet mother functions of the wavelet bases used
in the numerical experiments
4.
Some numerical experiments:
integral kernel sparsification, image compression and
reconstruction
5.
References
6.
Useful links
1.
Abstract
We present wavelet bases made of piecewise
(low degree) polynomial functions with an (arbitrary) assigned number of
vanishing moments. We study some of the properties of these wavelet bases; in particular we
consider their use in the approximation of functions and in numerical quadrature. We focus on two relevant applications: integral
kernel sparsification
and digital image compression and reconstruction. In these application
areas the use of the wavelet bases presented gives very satisfactory results. This website contains auxiliary
material and animations that help the understanding of the paper [10] and makes
available to the interested users some software programs that generate the
wavelet mother functions of the wavelet bases used to produce the numerical
results presented.
The numerical experience reported in this website and in the paper [10] has been obtained using the computing resources of CASPUR (Roma, Italy) under grant: “Algoritmi di alte prestazioni per problemi di scattering acustico”. The support and sponsorship of CASPUR are gratefully acknowledged.
2. Introduction
In the last few decades wavelets and wavelets
techniques have generated much interest, both in mathematical analysis as well as in signal
processing and in many other application fields. The link between the
mathematical analysis and signal processing approaches to the study of wavelets
was given by Coifman, Mallat
and Meyer (see [11], [12], [13],
[14], [15], [4]) with the introduction of multiresolution analysis and of the fast wavelet transform, and by Daubechies (see [6]) with the introduction of orthonormal bases of compactly supported wavelets.
Let A be an open subset of a real
Euclidean space and let 
be the Hilbert space
of the square integrable (with respect to Lebesgue measure) real functions defined on A. In
[10] when A is a sufficiently simple set (i.e. a parallelepiped in the
examples considered), starting from the notion of multiresolution
analysis, we construct wavelet bases of with an (arbitrary) assigned number of vanishing moments. In
this website we restrict our attention to the case A=(0,1). The main
feature of these wavelet bases is that they are made of piecewise polynomial
functions of compact support; moreover the polynomials used are of low degree
and generate bases with an arbitrarily high assigned number of vanishing
moments. This fact makes possible to perform very efficiently some of the most
common computations, such as, for example, differentiation and integration.
However the lack of regularity of the piecewise polynomial functions used can
create undesirable effects in the points
where the discontinuities occur when, for example, continuous functions are
approximated with discontinuous functions. Note that the wavelet bases
studied in [10], in general, make use of more than one wavelet mother
function. Thanks to these properties these wavelet bases in several
applications can outperform in actual computations the classical wavelet bases
and, for example, in [10] we show that they have very good approximation and
compression properties. The numerical results shown in Section 4 and in [10]
corroborate these statements both from the qualitative and the quantitative
point of view.
The wavelet bases introduced generalize the classical Haar's basis, that has only one vanishing moment and is
made of piecewise constant functions (see,
for example, [5]), and are a simple variation of the multi-wavelets bases introduced by Alpert in [1], [2]. The results reported here and in [10] extend those
reported in [7], [8]
and aim to show not only the theoretical relevance of these wavelet bases
(also shown, for example, in [1], [2],
[16], [17])
but also their effective applicability in real problems.
In particular in [10] we study some properties of the wavelet bases considered and the advantages
of using some of them in simple circumstances. In particular, the orthogonality of the wavelets to the polynomials up to a
given degree (i.e. the vanishing moments property) plays a crucial role in
producing “sparsity” in the representation using
these wavelet bases of functions, integral kernels, images and so on.
These wavelet bases as the wavelet bases
used previously have good localization properties both in the spatial and in
the frequency domains and can be used fruitfully in several classical problems
of functional analysis. In particular in [10] we focus on the representation of
a function in the wavelet bases and we
present some ad hoc quadrature formulae that can be used
to compute efficiently the coefficients of the wavelet expansion of a function.
We consider also the use of these wavelet bases in some applications, initially
we focus on integral kernel sparsification. This is a
relevant task, see for example [2], [3], since it makes possible, among other things, the approximation of
some integral operators with sparse matrices allowing the approximation and the
solution of the corresponding integral equations in very high dimensional
subspaces at an affordable computational cost. In [7], [8] and [9], for
example, we exploit this property to solve some time dependent acoustic
obstacle scattering problems involving realistic objects hit by waves of small
wavelength when compared to the dimension of the objects. Let us note that
these scattering problems are translated
mathematically in problems for the wave equation and that they are numerically
challenging, moreover thanks to the use of the wavelet bases, when boundary
integral methods or some of their variations are used, they can be approximated
by sparse systems of linear equations in very high dimensional spaces (i.e.
linear systems with millions of unknowns and equations).
Later on we focus on another important
application of wavelets: digital image compression and reconstruction. In this
framework, the basic idea is to distinguish between relevant and less relevant
parts of the image details disregarding, if
necessary, the second ones. In particular we proceed as follows: a
digital image is represented as a sequence of wavelet coefficients (wavelet
transform of the original image), a simple truncation procedure puts to zero
some of the calculated wavelet coefficients (i.e. those that are smaller than a
given threshold in absolute value) and keeps the remaining ones unaltered
(compression). The truncation procedure is performed in such a way that the
reconstructed image (i.e. the image obtained acting with the inverse wavelet
transform on the truncated sequence of wavelet coefficients) is of quality
comparable with the quality of the original image, but the amount of data
needed to store the compressed image is much smaller than the amount of data
needed to store the original image. In [10]
and in Section 4 we present some interesting numerical results in
wavelet-based image compression and reconstruction. Moreover we define a
compression coefficient to evaluate the
performances of the compression procedure and we study the behaviour
of the compression coefficients on some test problems, in particular we
show that the compression coefficients increase when the number of vanishing
moments of the wavelet basis used increases. This property can be exploited in
several practical applications.
A detailed exposition of the material
summarized in this website can be found in [10].
3.
Examples of MATLAB Symbolic Math codes that compute the wavelet mother
functions of the wavelet bases used in the numerical experiments
The MATLAB codes made available in this website
are: N0.m, N1.m, superN0.m, superN1.m. These programs build the wavelet
mother functions necessary to construct the wavelet bases of 
employed in the
numerical experiments of Section 4 and
in the numerical experiments presented
in [10]. The wavelet mother functions have been obtained using the Symbolic Math
Toolbox of MATLAB to implement the procedure described in [10].
In particular given the following parameters:
·
the
minimum number M of vanishing moments that the wavelet basis considered
must have,
·
the
number N of subintervals of the interval (0,1) employed and the
points 
, i=1,2,…,N-1, where the subdivision of (0,1) in
subintervals takes place,
the MATLAB code that constructs the specified
wavelet basis can be easily written generalizing the programs reported here.
We begin showing some wavelet basis functions 
, j=1,2,...,(N-1)M, obtained using as extra condition
the regularity criterion (for more details and for the definition of the
notation see [10]):
N0.m (download) J=M=1, N=2
and 
; (1)
N1.m (downoald) J=M=2, N=2
and.
(2)
The outputs of the programs N0.m, N1.m
are the equations
satisfied by the coefficients of the wavelet mother functions corresponding to
the choice of the parameters specified in (1) and (2) respectively. The
corresponding two non linear systems of equations have been solved with the
command solve of MATLAB. Let us note that all the
wavelet bases we present are uniquely
determined up to a “sign permutation” (for more details about the meaning of
“sign permutation” see [10]). One particular choice of this “sign
permutation” leads to the following mother functions used in the numerical
experience presented in Section 4:
Wavelet Basis 1: From (1) we obtain the mother function of the Haar’s basis:
Wavelet Basis 2: From (2) we obtain:
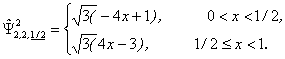
Note that the function 
is continuous in .
The Wavelet Basis 2 is one of the
multi-wavelets bases introduced by
Alpert in [1].
Some wavelet basis functions 
, j=1,2,...,(N-1)M, obtained using as extra condition
the “extra vanishing moments” criterion (for more details and for the
definition of the notation see [10]), are the following ones:
superN0.m (download) J=3, M=1, N=4
and 
=
, (3)
superN1.m (download)
J=6, M=2, N=4 and =.
(4)
The outputs of the programs superN0.m,
superN1.m are the
equations satisfied by the coefficients of the wavelet mother functions
corresponding to the choice of the parameters specified in (3) and (4)
respectively and a special choice of the request of “extra vanishing moments”.
The corresponding two non linear systems of equations have been solved with the
command solve of MATLAB.
These wavelet bases are uniquely determined up to a “sign permutation” as well. One
particular choice of this “sign permutation” leads to the following mother
functions used in the numerical experience presented in Section 4:
Wavelet Basis 3: From (3) we obtain:
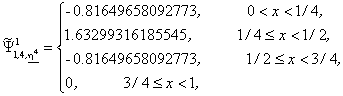
Let us note that 
and 
have two
vanishing moments while 
has only one vanishing moment.
Wavelet Basis 4: From (4) we obtain:
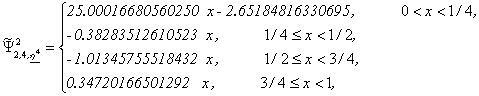
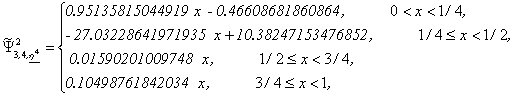
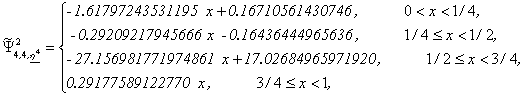
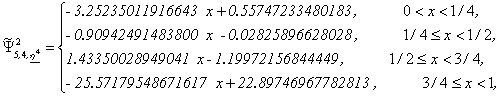
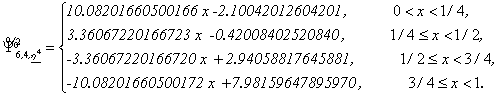
Let us note that 
, j=1,2,3,4,5,
have three vanishing moments while 
has only two
vanishing moments.
The choice of reporting in Section 4 and in [10]
the numerical results obtained with the Wavelet Bases 1, 2, 3, 4 is motivated
by the fact that these are the simplest bases among the bases introduced in [7] that it is possible to construct and
manipulate. Moreover the Bases 1 and 3 made of piecewise constant functions are
particularly well suited to deal with piecewise constant functions. This type
of functions is very important since it can be identified with digital signals
and images.
Note that the direct and inverse wavelet
transforms used in the numerical experience associated to these wavelet bases
have been implemented in FORTRAN 90.
4.
Some numerical experiments: integral kernel sparsification,
image compression and reconstruction
Integral kernel sparsification
In [10] we present some interesting properties
of the wavelet bases introduced. In particular we show how the representation
in these wavelet bases of certain classes of linear operators acting on 
may be viewed as a method for their “compression”, that is as
a method to approximate them with sparse matrices. In this way these operators can be applied to
arbitrary functions belonging to 
in a “fast” manner and
linear equations involving these operators can be approximated in high
dimensional spaces and solved at an affordable computational cost. Moreover we
show how the orthogonality
of the wavelets to the polynomials up to a given degree (the
vanishing moments property) plays a crucial role in producing these sparse
approximations. For more details see Theorems 4.1, 4.2 in [10].
In particular let 
be an integral
operator acting on of the form:
=
f 
, (5)
where the kernel K is a real function of
two variables. The compression algorithms we are interested in are based on the
following observation. When is represented on a wavelet basis, i.e. when the kernel K
is expanded as a function of two variables on the wavelet basis, the
calculation of the entries of the (infinite) matrix that represents the
operator in the wavelet basis involves
the evaluation of some integrals. If the wavelet basis considered has several
vanishing moments and we look at truncated wavelet expansions, that is to an
expansion on a truncated wavelet basis, when the kernel K is
sufficiently regular, thanks to the two estimates proven in the Theorems 4.1,
4.2 of [10], the fraction of the entries whose absolute value is smaller than a
chosen threshold approaches one when the truncated expansion approaches the
true expansion. The entries whose absolute value is smaller than a suitable
threshold can be set to zero committing a “small” error. This property makes
possible the approximation of the integral operator (5) with sparse matrices and makes possible to solve
numerically integral equations very efficiently.
Similar arguments can be made in the discrete
case, where we consider a piecewise
constant function defined on a bounded
rectangular domain of the form:
=
, (x,y) 
, i,j=1,2,…,r, (x,y) (0,1)
(0,1), (6)
where r
is a positive integer and h>0 is such that 
and where is the “pixel” of
indices i,j, i.e. =
, i,j=1,2,…,r. Note
that 
denotes the integer part of 
.
The comparison between the original and the
reconstructed “compressed” operator is made evaluating the relative difference
between the original and the reconstructed compressed kernels in the Frobenius-norm and it is very satisfactory. We indicate
with dim the dimension of the
vector space generated by the truncated wavelet basis and with
the compression coefficient obtained with our algorithm when
the truncation threshold 
>0 is used. The compression coefficient is defined as the ratio between dim2 and
the number of matrix elements whose absolute value exceeds a threshold >0.
Each frame of the animations that follow shows
four objects. Starting from the top left corner and moving in a clockwise sense
we show:
·
the
sparsity structure of the matrix obtained with the
specified basis when the threshold increases. In
particular the entries above the corresponding threshold in absolute value are shown in black;
·
the
compression coefficient ;
·
the
threshold ;
·
the
relative error in the Frobenius-norm made
substituting the original operator with the reconstructed “compressed” operator
after the truncation procedure as function of the threshold >0.
In [10] some tables comparing the compression
coefficients for different values
of the threshold are shown.
Example 1.
In this
example we consider the kernel:
and we expand it in the Wavelet Bases 2 and 4
generated by the mother functions reported in Section 3. We set to zero the
entries of the resulting matrix whose absolute value is smaller than the
threshold >0 and, when increases, we obtain
the results shown in Animations 1 and 2.
Animation 1. Example 1: Sparsity structure of the matrix
obtained with the Wavelet Basis 2 for dim=512.
Animation 2. Example 1: Sparsity structure of the matrix
obtained with the Wavelet Basis 4 for dim=512.
Example 2.
In this
example we compress the following piecewise constant function:
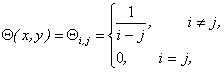(x,y) , i,j=1,2,…,dim,
and 
, (x,y) (0,1)(0,1),
where is the “pixel” of
index i,j, defined previously. Remind that . Animation 3 and 4
show some numerical results relative to Example 2 when dim=256 and we
use the Wavelet Bases 1 and 3 generated by the mother functions reported in
Section 3 respectively.
Animation 3. Example 2: Sparsity structure of the matrix
obtained with the Wavelet Basis 1 for dim=256.
Animation 4. Example 2: Sparsity structure of the matrix
obtained with the Wavelet Basis 3 for dim=256.
Image compression and
reconstruction
We
consider here some applications of the wavelet bases constructed in
Section 3 in image compression and reconstruction. In particular we show some
reconstructions of images and we focus
on a lossy
compression procedure. We limit our attention to grayscales
images. Despite the appearance, compressing grayscale
images is more difficult than compressing colour images. In fact human visual
perception can distinguish more easily brightness (luminance) than colour
(chrominance).
Going into details the steps in our image
compression and reconstruction scheme are the following:
- digitize the original image
(i.e. transform the image in a matrix of numbers),
- apply the wavelet
transform to represent the image
through a set of wavelet coefficients,
- manipulate (i.e. set to zero)
some of the wavelet coefficients,
- reconstruct the image with the
inverse wavelet transform.
Note that the step 3 is the key step. In fact
the lossy compression step is based on the fact that
many of the wavelet coefficients are small in absolute value, so that they can
be set to zero with little damage to the image. This procedure is called thresholding. In practice the most simple thresholding procedure consists in choosing a fixed
tolerance and in doing the following truncation procedure: the wavelet
coefficients whose absolute value falls below the tolerance are put to zero.
Only the non zero wavelet coefficients after the thresholding
procedure are used to build the so called compressed image. The goal is to
introduce as many zeros as possible without losing a great amount of details.
The crucial issue consists in the choice of
the threshold.
The following animations show three objects. In
particular starting from the top left corner and moving in a clockwise sense we
show:
·
the
variation of the compressed images obtained with the specified wavelet basis
according to the value of the threshold ;
·
the
compression coefficient ;
·
the
threshold ;
To see only the behaviour of the compressed
images please click on the right button.
In [10] some tables comparing the compression
coefficients for different values
of the threshold are shown.
Example 3.
In this
example we consider the image of Figure
1 which is the famous Lena image. This image has 256x256
pixels.
|
|
|
Figure
1. Lena: Original image |
In Animation 5- 7 we show for different wavelet
bases and several choices of the parameter dim how the “compressed Lena image” improves when
the threshold decreases. Note that
if all the wavelet coefficients are used in the
inverse wavelet transform (or equivalently, if we take the threshold equal to zero) and
an exact arithmetic is used the original image can be reconstructed exactly.
Animation 5. Example 3: Compressed images with the Wavelet Basis 3 when dim=64
and the threshold decreases.
Animation 6. Example 3: Compressed images with the Wavelet Basis 3 when dim=256
and the threshold decreases
Animation 7. Example 3: Compressed images with the Wavelet Basis 4 when dim=512
and the threshold decreases
Example 4.
We consider
the image of Figure 2. In this image are evident three different types of
objects: a shape (the black star), a number ('2025') and an inscription
('black'). This image has 278x268 pixels.
|
|
|
Figure
2. Original image |
The following Animations 8-9 show the
compressed images of Figure 2 obtained for dim=128 and the Wavelet Bases
2, 4 when the threshold decreases. Finally
Animation 10 shows the compressed images of Figure 2 obtained for dim=256
and using the Wavelet Basis 3 when the threshold decreases.
Animation 8. Example 4: Compressed images with the Wavelet Basis 2 when dim=128
and the threshold decreases
Animation 9. Example 4: Compressed images with the Wavelet Basis 4 when dim=128
and the threshold decreases
Animation 10. Example 4: Compressed images with the Wavelet Basis 3 when dim=256
and the threshold decreases.
5.
References
[1] B.K. Alpert, Wavelets and other bases for fast numerical linear algebra, in Wavelets: a tutorial in theory and applications, C. K. Chui, Editor, Academic Press, New York, (1992), pp. 181-216.
[2] B.K. Alpert, A class of bases in L2 for the sparse representation of integral operators, SIAM J. Math. Anal., 24(1) (1993), pp. 246-262.
[3] B.K. Alpert, G. Beylkin, R.R. Coifman, and V. Rokhlin,
Wavelet-like bases for the fast solution of second-kind integral equations, SIAM J. Sci. Comp., 14 (1993), pp. 159-184.
[4] R.R. Coifman, Y. Meyer, Ondelettes et Opérateurs
III: Opérateurs multilinéaires, Hermann, Paris, 1991.
[5] I. Daubechies, Ten
Lectures on Wavelets, SIAM, Philadelphia, Pennsylvania, 1992.
[6] Daubechies, Orthonormal bases of compactly supported wavelets, Comm. Pure Appl. Math, 41 (1998), pp. 909-996.
[7] L. Fatone, M.C. Recchioni,
and F. Zirilli,
New scattering problems and numerical methods in acoustics, in Recent
Research Developments in Acoustics, S.G.Pandalai Managing Editor, Transworld
Research Network, Kerala, India, 2, 2005, pp. 39-69.
[8] L. Fatone, G. Rao, M.C. Recchioni, and F. Zirilli, High
performance algorithms based on a new wavelet expansion for time dependent
acoustic obstacle scattering, Comm.
Comp. Phys. (2007), 2(6) (2007), pp. 1139-1173.
[9] L. Fatone, M.C. Recchioni, and F. Zirilli, A
numerical method for time dependent acoustic scattering problems involving
smart obstacles and incoming waves of small wavelengths, in Mathematical Modeling
of Wave Phenomena, B.Nilsson, L.Fishman Editors,
AIP Conference Proceedings, 834 (2006), pp.108-121.
[10] L. Fatone, M.C. Recchioni, and F. Zirilli, Wavelet bases made of piecewise polynomial functions: approximation theory, quadrature rules and applications to integral kernel sparsification
and image compression, Applied Mathematics, 2 (2011) , pp.196-216.
[11] S. Mallat, Multiresolution approximation and wavelets,
Trans. Amer. Math. Soc., 315 (1989), pp. 69-88.
[12] S. Mallat, Multifrequency channel decompositions of images
and wavelet models, IEEE Trans. Acoust. Speech
Signal Process., 37 (1989), pp.
2091-2110 .
[13] Y. Meyer, Ondelettes, fonctions splines et analyses graduées, Rend. Sem. Mat. Univ. Politec. Torino, 45 (1988), pp.1-42.
[14] Y. Meyer, Ondelettes et Opérateurs I:
Ondelettes, Hermann, Paris, 1990.
[15] Y. Meyer, Ondelettes et Opérateurs II:
Opérateurs de Calderón-Zygmund, Hermann, Paris, 1990.
[16] C.A. Micchelli and Y. Yu, Using the matrix refinement equation for the construction of wavelets on invariant sets, Appl. Comp. Harmonic Anal., 1 (1994), pp.391-401.
[17] C.A. Micchelli and Y. Yu, Reconstruction and decomposition algorithms for biorthogonal multiwavelets, Multidim. Syst. Sign. Process., 8 (1997), pp. 31-69.
6.
Useful links
http://www.econ.univpm.it/recchioni/scattering/w12
http://www.econ.univpm.it/recchioni/scattering/w14
http://www.econ.univpm.it/recchioni/scattering