HIGH PERFORMANCE ALGORITHMS FOR TIME DEPENDENT WAVE SCATTERING FROM A BOUNDED OBSTACLE^\dag

Maria Cristina Recchioni

Istituto di Matematica e Statistica

Università di Ancona

Piazza Martelli, 60121 Ancona, Italy

e-mail : recchioni@posta.econ.unian.it

Francesco Zirilli

Dipartimento di Matematica "G. Castelnuovo"

Università di Roma "La Sapienza"

00185 Roma, Italy

e-mail : f.zirilli@caspur.it

Abstract

We present a numerical method to compute the solution of a time dependent three dimensional scattering problem for the wave equation. That is given a bounded simply connected obstacle having a known constant acoustic impedance find the scattered wave generated by an incoming wave packet that hits the obstacle. The scattered wave is obtained as the solution of an exterior problem for the wave equation, and is computed as a superposition of time harmonic waves. Each time harmonic wave is computed using the operator expansion method [1]. The method we present is highly parallelizable both with respect to the time and the space variables. In fact the computation of the time harmonic waves can be carried out in parallel and a high level of parallelism can be used in the computation of each time harmonic wave via the operator expansion method. Numerical results on test problems obtained with a parallel implementation of the numerical method proposed here are shown. A discussion of the results both from the numerical and from the physical point of view is given. Some animations of the numerical results obtained are shown.

1 Introduction

Let R be the set of real numbers, R³ be the three dimensional real euclidean space and x = (x,y,z)^T Î R³ be a generic vector, where the superscript T means transposed. Let (·,·), ||·|| denote the Euclidean scalar product in R³ and the corresponding Euclidean vector norm respectively. Let W Ì R³ be a bounded simply connected open set with locally Lipschitz boundary ¶W, i.e. for example a polyhedron, and let `W be its closure. We assume that the origin of the coordinate system lies inside W, that is there exists a > 0 such that B<sub>a</sub>, the sphere of center the origin and radius a, is contained in W, we can also assume that `B_a Ì W. We note that when ¶W is a locally Lipschitz boundary the outward unit normal vector to ¶W, n( x) = (n₁( x),n₂( x),n₃( x))^T Î R³,  x Î ¶W, exists almost everywhere in x when x Î ¶W, (see [2], Lemma 2.42, p. 88). We consider acoustic waves propagating in a homogeneous isotropic medium in equilibrium at rest filling R³\W, where W is the scatterer that we assume to be characterized by a constant boundary acoustic impedance c ³ 0 (see [3] p. 66), and we assume that no source terms are present. Let uⁱ( x,t), ( x,t) Î R³×R be the incoming wave, in the small amplitude approximation we can assume that uⁱ( x,t) satisfies (see [4], chap. 6, p. 243):

where D = ¶²/¶x²+¶²/¶y²+¶²/¶z² is the Laplace operator and c > 0 is the wave propagation velocity. The scattered wave u^s( x,t), ( x,t) Î (R³\`W)×R, generated when the incoming wave hits the obstacle W, is the solution of the following equation:

where r = || x||, x Î R³ and O(·) and o(·) are the Landau symbols. Note that the function g( x,t) is defined almost everywhere. We note that the boundary condition (1.3) contains as limit cases the acoustically soft obstacle, that is c = 0, and the acoustically hard obstacle, that is c = ¥, and that the boundary condition at infinity (1.5) and the radiation condition (1.6) imply that u^s( x,t) as r ® +¥ is made to leading order only of outgoing waves (see [5] p. 485). It is easy to see that when we choose the incoming wave to be a time harmonic wave, that is:

We note that the function b_w ( x) in general is defined only almost everywhere in x for x Î ¶W and that equations (1.9), (1.12) imply that u_w^s = O(1/r) as r® ¥. The exterior boundary value problem (1.9), (1.10), (1.12) has an unique solution for each w when c ³ 0 and ¶W is a locally Lipschitz surface (see [6] Lemma 9 p. 37, and Appendix 1 p. 325). Since uⁱ( x,t) solves (1.1) in R³×R it can be represented as a superposition of time harmonic waves of the form (1.7) with uⁱ_w ( x) = e^{i(w/c)( x, a)} , a Î R³, || a || = 1, and we can assume that the scattered wave can be represented in a similar way, that is:

where ¶B is the boundary of the sphere of center the origin and radius one, ds( a) is the surface measure on ¶B, and W(w, a), (w, a) Î R׶B , is a suitable distribution that in equation (1.14) plays the role of a normalization factor. In several applications (see Section 3) W(w, a) has support in { (w, a ) Î R׶B  |  a = g,  g Î ¶B } so that the integrals (1.13), (1.14) reduce to one dimensional integrals. Substituting (1.13), (1.14) into (1.2), (1.3), (1.5), (1.6) it follows that for w Î R, a Î ¶B, u_{w, a} ^s( x) satisfies the exterior boundary value problem (1.9), (1.10), (1.12) with uⁱ_w ( x) = e^{i(w/c)( x, a)}, x Î R³, w Î R, a Î ¶B. The method proposed in Section 2 to solve problem (1.2), (1.3), (1.5), (1.6) is based on a quadrature rule to approximate the integrals in (1.13), (1.14) and on the operator expansion method to compute the time harmonic waves u_{w, a} ^s that appear in the quadrature rule (see [1]). Formula (1.14) provides the possibility to have a numerical method to approximate u^s( x,t) with high parallel performance since the computation of the space dependent parts u_{w, a} ^s of u^s and of the time dependent parts e^-iwt of u^s, w Î R, a Î ¶B are independent one from the other and can be carried out in parallel. Moreover as shown in Section 2 the computation of each time harmonic wave u_{w, a} ^s is carried out efficiently in parallel via the operator expansion method.

The operator expansion method used here was originally introduced by Milder [7] in the case of time harmonic acoustic scattering from an unbonded surface and then it was generalized to the case of time harmonic electromagnetic scattering from an unbounded surface by Milder [8], Smith [9], Piccolo, Recchioni, Zirilli [10]. Later Misici, Pacelli, Zirilli [11] introduced a new formalism for time harmonic acoustic scattering from a bounded surface and this formalism was generalized to the electromagnetic case by Fatone, Pignotti, Recchioni, Zirilli [12]. Finally Mecocci, Misici, Recchioni, Zirilli [1] considered the problem of time dependent acoustic scattering from a bounded obstacle.

In Section 2 we present the algorithm used to solve the acoustic three dimensional time dependent problem (1.2), (1.3), (1.5), (1.6). This algorithm is only one example of the highly parallelizable algorithms that can be obtained using the ideas described here to solve several scattering problems. In Section 3 we show some numerical results obtained with a parallel implementation of the algorithm presented in Section 2. A brief discussion of the numerical results both from the numerical and the physical point of view is given and some animations of the numerical results are shown. Some other animations of similar results can be found in the website: http://www.econ.unian.it/recchioni/w1 .

2 The algorithm for the time dependent scattering problem

Let us consider the exterior problem for the wave equation (1.2), (1.3), (1.5), (1.6). The algorithm we present approximates the integral (1.14) using a quadrature rule that is the solution u^s( x,t) is given by the following superposition of time harmonic waves:

where N₁, N₂ are positive integers, a_i,j, w_i, a_j, i = 1,2,¼,N₁, j = 1,2,¼,N₂ are coefficients and nodes of the chosen quadrature rule and Error is the error term (see [1] formulae (1.17), (1.19)). For i = 1,2,¼,N₁, j = 1,2,¼,N₂, (w_i, a_j) Î R׶B, it is easy to see that u^s_{wi, aj} is the solution of the exterior boundary value problem (1.9), (1.10), (1.12) with w = w_i, and uⁱ_wi( x) = e^{i(w_i/c) ( x, a_j)}. Let (w, a) Î R׶B, we assume that the solution u_{w, a} ^s of (1.9), (1.10), (1.12) can be extended to R³\`B<sub>a</sub>, where B<sub>a</sub> is the sphere chosen in Section 1, that is such that `B_a Ì W, and we assume that this extension F_{w, a}( x) can be represented as follows:

is the free space Green's function of the Helmholtz operator with the Sommerfeld radiation condition at infinity. It is easy to see that independently from the choice of the density function v_{w, a}(^y) the function F_{w, a}( x) satisfies the Helmholtz equation (1.9) and the radiation condition (1.12). So that we determine v_{w, a}(^y) imposing that F_{w, a}( x) satisfies the boundary condition (1.10) that is:

Let (r,q,f) be the usual spherical coordinates in R³ and let W be a starlike domain with respect to the origin, that is there exists a positive single valued function x defined on ¶B such that:

where 0! = 1, and the coefficients v_{s,w, a}(^ x),  ^x Î ¶B, s = 0,1,¼, are to be determined. Substituting (2.6), (2.7) into equation (2.4) we can determine v_{s,w, a}(^ x), ^x Î ¶B, s = 0,1,¼ solving order by order the resulting equation, that is solving the following integral equations:

and the functions z_{s,w, a}(^x), ^x Î ¶B, s = 1,2,¼ are obtained equating in (2.4) the coefficients that multiply the same powers of x-1 (see [1] Lemma 2.2). We note that the integral equations (2.8) are defined on ¶B so that to solve them we can make use of the real spherical harmonics functions Y_s,l,m(^x), ^x Î ¶B, s = 0,1, l = s,s+1,¼, m = s,s+1,¼,l, (see [3], p. 77). These functions are an orthonormal complete set of functions of L²(¶B). Let us remind the following formula:

Lemma 2.1: Let c > 0, let z_{s,w, a}(^x), ^x Î ¶B, a Î ¶B, w Î R, s = 0,1,¼, be the functions that appear in (2.8) and let

be the expansion in spherical harmonics of the function z_{s,w, a}(^x), then the function F_{w, a}( x) given by (2.2) solution of (1.9), (1.10), (1.12) has the following expansion:

Proof: See [1] Lemma 3.4. We note that equation (2.12) must be slightly modified when c = 0 or c = ¥ as shown in [1].

Roughly speaking we choose the basis of real spherical harmonics since this basis makes the infinite matrices that represent the action of the integral operators in (2.8) diagonal. We can see this fact substituting formula (2.10) in (2.8), multiplying both sides of equation (2.8) for a fixed spherical harmonics function Y_{s^¢,l^¢,m^¢} and finally integrating over ¶B. We note that the perturbative solution of (2.4) makes the resulting integral equations (2.8) easy to solve in fact their solution can be reduced to the solution of a set of diagonal linear systems. Moreover the perturbative expansion attenuates the smoothing effect contained in the reduction of the problem from being an integral equation on ¶W to being an integral equation on ¶B. The use of a boundary integral method to solve problem (1.9), (1.10), (1.12) implies the solution of an integral equation on ¶W that translates in a computational expensive linear system. Furthermore the computation of the coefficients z_{s,w, a, s,l,m}, s = 0,1, l = s,s+1,¼, m = s,s+1,¼,l for each fixed value of s, s = 0,1,¼, can be carried out in parallel since they are given by double integrals independent one from the others, i.e.:

We note that formula (2.14) makes the computation of the space dependent part of u^s( x,t), i.e. u_{wi , aj}^s( x), i = 1,2,¼,N₁, j = 1,2,¼,N₂ independent from the computation of the time dependent part of u^s( x, t), i.e. e^{-iw_i t}, i = 1,2,¼,N₁. Furthermore the computation of u_{wi , aj}^s( x), i = 1,2,¼,N₁, j = 1,2,¼,N₂ is carried out in parallel since they are solutions of independent boundary value problems of the type (1.9), (1.10), (1.12), and the computation of each u_{wi , aj}^s( x) is highly parallelizable in fact at any fixed order s, s = 0,1,¼ the computation of z_{s,wi, aj, s,l,m} is carried out simultaneously in s = 0,1, l = s, s+1, ¼, m = s, s+1,¼,l. Finally the solution of the corresponding diagonal linear system can be carried out in parallel and this structure of the computation makes it highly parallelizable with respect to time and space variables.

3 Numerical experience

In this section we use the algorithm presented in Section 2 to solve the time dependent acoustic scattering problem (1.2), (1.3) (1.5) (1.6) in some test cases. We consider the scattering phenomenon generated by an incident acoustic wave that hits an obstacle W when the incident acoustic wave is a time harmonic plane wave:

where g Î ¶B, z ¹ 0, w^* Î R are given. In all the experiments we choose g = (0,0,-1)^T, c = 1, and ¶B as base point of the perturbative expansion (see (2.6)). We remark that the sphere B_a Ì W (see (2.2)) does not have a real use in the computational method (see (2.14) and [1] Lemma 3.4). In the experiments involving the incident wave (3.2) we choose the quadrature rule (2.1) to be the Gauss Hermite quadrature rule (see [14] p.114) with N₂ = 1, a₁ = g, with w_i, i = 1,2,¼,N₁, to be the zeros of the Hermite polynomial of degree N₁ and a_i,1, i = 1,2,¼,N₁, to be the weights of the Gauss Hermite quadrature formula. We choose N₁ = 400 (see [1] Section 4).

When we use the incident wave (3.1) no quadrature rule in the variables w, a are involved since the scattered wave has the form (1.8) with w = w^*. We note that when the time harmonic incoming wave (3.1) hits a sphere of radius one and center the origin the space dependent part of the corresponding time harmonic scattered wave coincides with the zeroth order term of the expansion in powers of x-1 given by (2.12). We truncate the series expansion (2.12) in spherical harmonics at a given value of l, l = L_max and the series expansion in powers of x-1 at a given value of s, s = S. In the numerical experience presented here we choose L_max = 16 (see [1] Section 4), and we consider several values of S. The same experiments with L_max > 16 give numerical results that agree with the ones presented here to at least three decimal digits.

The algorithm previously described has been coded in Fortran 90 language and tested on a Cray T3E machine with 128 processors in "Single Program Multiple Data" programming mode using MPI as "message passing" library.

We consider two obstacles: the double cone:

where h > 0 is a real parameter. The double cone and the corrugated sphere are obstacles with Lipschitz continuous boundary, in particular these boundaries are not continuously differentiable. We begin discussing the numerical experiments from the numerical point of view and we show some evidence of the quantitative character of the results obtained with the expansion introduced in the previous section. We consider the incident wave (3.1). The following Table 3.1 shows the "numerical" convergence of the formal series expansion in powers of x-1 of the function F_{w^* , a} given by (2.12), where a = g = (0,0,-1)^T, w^*/c = 10. From (2.12) we have:

From Tables 3.1 we can see that the convergence of the series expansion in powers of x-1 in (2.12) depends on the magnitude of h. A more accurate observation shows that the convergence depends on the magnitude of (w^*/c)max_{^ x Î ¶B}|x(^ x)-1|, and in the examples considered the convergence is satisfactory roughly when (w^*/c)max_{^ x Î ¶B}|x(^ x)-1| £ 1.5. The first two rows of Table 3.1 show that the ``operator expansion'' method used to compute the time harmonic waves in favourable circumstances gives very accurate results. We do not discuss the convergence of the ``Fourier integral'' (1.14) that gives u^s( x,t) or the validity of the Gauss-Hermite quadrature rule used to approximate it since these are standard topics in analysis.

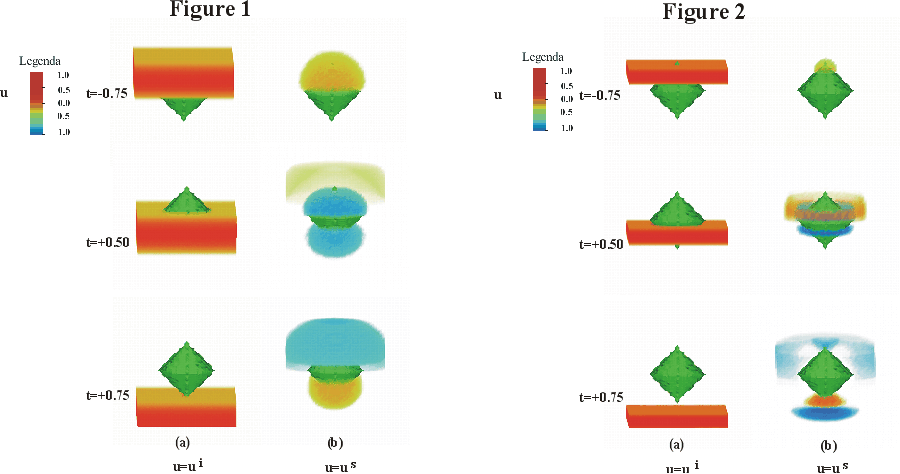
We show now an experiment which is interesting from the physical point of view. We consider the double cone given by (3.3) and the incident wave (3.2). Let

in the following animations and figures we show in the first column the scale of colour of u, in the second column the incident wave u = uⁱ( x,t) (3.2) (Figures 1(a), 2(a)) and in the third column the scattered wave u = u^s( x,t) (Figures 1(b), 2(b)) solution of (1.2), (1.3), (1.5), (1.6) on the spatial grid Z₄₀. This is done for twenty values of the time t, t = -2+0.25*j, j = 0,1,¼,19 and finally repeated five times in each animation. The figures show three values of t, that is t = -0.75, t = 0.5, t = 0.75. When times goes on we can see that the incident wave uⁱ( x,t) goes through the obstacle. This scene is repeated five times in the animations. The experiment in the animations and in the figures shows the behaviour of the scattered wave u^s( x,t) solution of (1.2), (1.3), (1.5), (1.6) generated by the acoustically hard (c = ¥) double cone when hit by the incident wave uⁱ( x,t) given by (3.2) with z² = 1/4 (Animation 1, Figure 1), or with z² = 1/64 (Animation 2, Figure 2). In this experiment we use S = 8 in (2.14). We can see that when z² is large (i.e.: z² = 1/4 ) the entire surface of the double cone irradiates energy (Animation 1, Figure 1) while when z² is small (i.e.: z² = 1/64) we can see that most of the energy is irradiated by the vertices and the edge of the double cone (Animation 2, Figure 2). The reason of this phenomenon lies in the fact that when z² decreases the components of high frequency of the incident wave packet become more relevant.

Table 3.2 shows the time required by the algorithm on the Cray T3E machine to execute the computation of å_{s = 0}⁸ z_{s,wi, g,s,l,m} (see (3.5)), with g = (0,0,-1)^T, i = 1,2,¼,N₁, s = 0,1, l = s,¼, L_max, m = s,¼,l, N₁ = 400, L_max = 16 relative to an acoustically hard double cone (3.3) versus the number of processors used. The time is measured using the (Fortran) routine rtc() of the Cray T3E machine that gives the real time clock in clicks where a click corresponds to 3.333e-09 seconds.

Table 3.2 shows that when the number of the processors is multiplied by a factor 2 the time required to execute the computation is divided roughly by the same factor, that is the numerical algorithm shows a high parallel performance.

Some animations relative to some other numerical experiments can be found in the website http://www.econ.unian.it/recchioni/w1 .

[1]

E. Mecocci, L. Misici, M.C. Recchioni, F. Zirilli: "A new formalism for time dependent wave scattering from a bounded obstacle", submitted to Journal of the Acoustical Society of America.

[2]

J. Neas: "Les Méthodes Directes en Théorie des Équations Elliptiques", Masson & Cie. Publ., Paris, 1967.

[3]

D. Colton, R. Kress: "Integral Equation Methods in Scattering Theory", J.Wiley & Sons Publ., New York, 1983.

[4]

P.M. Morse, K.V. Ingard: "Theoretical Acoustics", Mc Graw Hill Inc., New York, 1968.

[5]

J.A. Stratton: "Electromagnetic Theory", McGraw-Hill Book Company, New York, 1941.

[6]

A.G. Ramm: "Scattering by Obstacles", D. Reidel Publishing Company, Dordrecht, Holland, 1986.

[7]

D.M. Milder: "An improved formalism for wave scattering from rough surface", Journal of the Acoustical Society of America, 89, 1991, 529-541.

[8]

D.M. Milder: "An improved formalism for electromagnetic scattering from a perfectly conducting rough surface", Radio Science, 31, 1996, 1369-1376.

[9]

R.A. Smith: "The operator expansion formalism for electromagnetic scattering from rough dielectric surfaces", Radio Science, 31, 1996, 1377-1385.

[10]

S. Piccolo, M.C. Recchioni, F. Zirilli: "The time harmonic electromagnetic field in a disturbed half-space: An existence theorem and a computational method", Journal of Mathematical Physics,37, 1996, 2762-2786.

[11]

L. Misici, G. Pacelli, F. Zirilli: "A new formalism for wave scattering from a bounded obstacle", Journal of the Acoustical Society of America, 103, 1998, 106-113.

[12]

L. Fatone, C. Pignotti, M.C. Recchioni, F. Zirilli: "Time harmonic electromagnetic scattering from a bounded obstacle: An existence theorem and a computational method", to appear in Journal of Mathematical Physics.

[13]

M.Abramowitz, I.A.Stegun: "Handbook of Mathematical Functions", Dover Publications Inc., New York, 1970.

[14]

A.Ghizzetti, A. Ossicini: "Quadrature Formulae", Birkhäuser Verlag, Basel, 1970.

• Paper Figure 1 ( File GIF - 280K )

• Paper Figure 2 ( File GIF - 280K )

• Paper Figures 1-2 ( File GIF - 380K )

 

ANIMATION 1: uⁱ = e^-(z+t)2

• Animation 1 ( File GIF - 876K )

 

ANIMATION 2: uⁱ = e^-16(z+t)2

• Animation 2 ( File GIF - 753K )

 

 

 

---

Footnotes:

^\dag The numerical experience shown in this paper has been made possible by the support and sponsorship of CINECA - Casalecchio di Reno (BO) - Italy through a grant account on the T3E computer facility.

---

File translated from T_EX by T_TH, version 1.30.