The use of the Pontryagin maximum principle in a furtivity problem in time dependent acoustic obstacle scattering
Francesca Mariani
Dipartimento di Matematica e Fisica
Università di Camerino
Via Madonna delle Carceri, 62032 Camerino (MC), Italy
e-mail : fdmariani@libero.it
Maria Cristina Recchioni
Istituto di Teoria delle Decisioni e Finanza Innovativa
Università di Ancona
Piazza Martelli 8, 60121 Ancona, Italy
e-mail : recchioni@posta.econ.unian.it
Francesco Zirilli
Dipartimento di Matematica "G. Castelnuovo"
Università di Roma "La Sapienza"
00185 Roma, Italy
e-mail : f.zirilli@caspur.it
In this paper we consider a furtivity problem in the context of time dependent three dimensional acoustic obstacle scattering. The scattering problem for a "passive" obstacle is the following: an incoming acoustic wave packet is scattered by a bounded simply connected obstacle with locally Lipschitz boundary having a known boundary acoustic impedance. The scattered wave is the solution of an exterior problem for the wave equation. To make the obstacle furtive we leave "passive" obstacles and we consider "active" obstacles, that is obstacles that when hit by the incoming wave packet react circulating on their boundary a pressure current. The furtivity problem consists in making the acoustic field scattered by the obstacle "as small as possible" choosing a control function, that is a pressure current on the boundary of the obstacle, in the function space of the admissible controls. That is it consists in finding the control function that minimizes a cost functional that will be made precise later. This furtivity problem is of great relevance in many applications.
The mathematical model for this furtivity problem consists in a control problem for the wave equation. That is in the boundary condition for the wave equation on the boundary of the obstacle we introduce a control function that is the so caled pressure current. The cost functional depends on the control function, and on the scattered acoustic field. Note that the scattered field depends on the control function via the boundary conditions. Using the Pontryagin maximum principle we prove that, for a suitable choice of the cost functional, the first order optimality conditions for the furtivity problem considered can be formulated as an exterior problem defined outside the obstacle for a system of two coupled wave equations. To solve this exterior problem we develop a highly parallelizable numerical method based on a "perturbative series" of the type proposed in [1]. This method obtains the time dependent scattered field and the control function as a superposition of time harmonic functions. The space dependent parts of each time harmonic component of the scattered field and of the control function are obtained solving a boundary value problem for two coupled Helmholtz equations. The mathematical model and the numerical method proposed are validated studying numerically some test problems. The results obtained with a parallel implementation of the numerical method proposed on the test problems are shown and discussed from the numerical and the physical point of view. The quantitative character of the results obtained is established.
In the following gif animations from left to right we show the colour scale, the incident wave, the scattered wave from the "passive" ostacle, the scattered wave from the "active" obstacle and (in Animation 1) the control variable divided by 10.
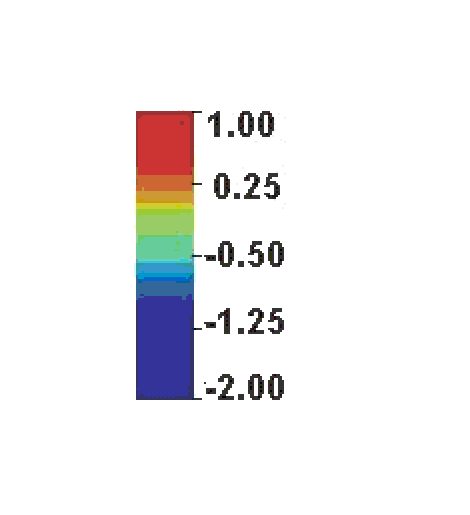
In the following mpeg animations from left to right we show the incident wave, the scattered wave from the "passive" ostacle and the scattered wave from the "active" obstacle. The colour scale used in the mpeg animations is the following one:

Obstacles animations 1 and 2:

The sound presented in the following mpeg animations is a synthetic sound that simulates the sound heard by an observer located in the observation point suggested by the view angle of the animation.
 File mpeg - 376K )
File mpeg - 376K ) File mpeg - 376K )
File mpeg - 376K ) File mpeg - 376K )
File mpeg - 376K )
 File mpeg - 136K )
File mpeg - 136K )