PAPER:
Maximum likelihood
estimation of the parameters of a system of stochastic differential equations
that models the returns of the index of some classes of hedge funds*
Lorella Fatone, Francesca Mariani, Maria
Cristina Recchioni, Francesco Zirilli
- Abstract
- Introduction
- Filtering problem Filtering Movies
- Estimation
problem Estimation
Movies
- References
- FORTRAN code
Warning: If your
browser does not allow you to see the content of this website click here to download a word file that reproduces the material contained here.
*The numerical experience reported in this paper has been obtained using
the computing grid of ENEA (
In [1] we study an inverse problem for a parabolic
partial differential equation. The parabolic partial differential equation
considered is the Fokker Planck equation
associated to a system of stochastic
differential equations and the inverse problem studied consists in finding from
suitable data the values of the parameters that appear in the coefficients of
this Fokker Planck equation, that is of the parameters that define the system
of stochastic differential equations. The data used in the reconstruction of
the parameters are observations made at discrete times of the stochastic process solution of the
system of stochastic differential equations. That is, the data of the inverse
problem are a “sample” taken from some of the components of the vector solution
of the stochastic differential equations and not, as usual, observations made
on the solution of the parabolic equation. The choice of the system of
stochastic differential equations and of the data used in the inverse
problem are motivated by applications in
mathematical finance. The stochastic differential equations presented can be
used to model the dynamics of the log-returns
of the index of some classes of hedge funds, such as, for example, the so
called “long short equity” hedge funds
and of some auxiliary variables. The
solution of the inverse problem proposed is obtained through the solution
of a filtering and of an estimation
problem. The solution of the last two problems is based on the knowledge of the
joint probability density function of the state variables of the model
conditioned to the observations made and
to the initial condition. This joint
probability density function is solution of an initial value problem for the
Kushner equation that in the circumstances considered here can be written as a
sequence of initial value problems with appropriate
initial conditions for the Fokker Planck equation associated to the system of
stochastic differential equations. An integral representation formula for this
probability density function is derived and used to develop a numerical
procedure to solve the estimation problem using the maximum likelihood method.
The computational method proposed has been tested on synthetic data and the results obtained are presented. This
website contains some auxiliary material useful to understand [1]
and contains some animations and the description of some numerical experiments. A more general
reference to the work of the authors and of their coauthors in mathematical
finance is the website: http://www.econ.univpm.it/recchioni/finance.
Assuming
the log-return of the stock prices index, the log-return of the index of a
suitable class of hedge funds (i.e.: for
example “long short equity” class) and
the stochastic variance of the
stock prices index as state
variables and the log returns of the index of the stock prices and of the index of the hedge funds class observed
at discrete times as observations, we study the problem of forecasting
(tracking) the unobserved and time-varying stochastic variance when the model
parameters and initial condition are known using the observations (filtering
problem) and the problem of estimating the model parameters and the unknown initial stochastic variance using the observations (estimation
problem). The solution of this last problem is needed in order to use the
model proposed to forecast in real
situations future log returns of the stock prices and hedge funds indices.
Let
xt , zt, and vt be the state variables at time
t>0 that is, respectively, the log-return of stock prices index, the log-return of the
index of the hedge funds class and the stochastic variance of the stock prices index
at time t>0. We assume that the stochastic process (xt , zt
, vt ), t>0, is solution of
the following system of stochastic differential equations:
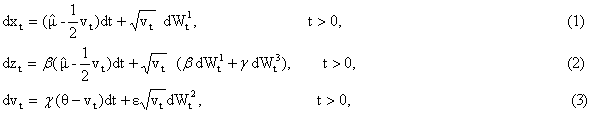
where Wt1, Wt2,
Wt3 , t>0, are standard Wiener processes such that W01=W02=
W03 =0, dWt1,
dWt2 , dWt3 , are their stochastic
differentials and <dWt1dWt2
>= r1,2dt, <dWt1dWt3
>= r1,3dt, <dWt2dWt3
>= r2,3dt
where < × > denotes the mean of × and r1,2,r1,3,r2,3Î[-1,1] are constants known as correlation coefficients, ![]() is a real constant
related to the behaviour of the mean of the stock prices index log return,
associated to the stochastic process of the stock prices index St
, t>0. Note that the stochastic
variance vt, t>0, is
assumed to be described by a mean-reverting process with speed c³0 and parameters q³0 and e³0, that is by equation (3). The stochastic differential equations (1), (3) are
known as Heston model [2]. Equation (2) has been
introduced to model the log-returns of the indices of suitable classes of hedge
funds (such as, for example, the long short equity class). In fact equation (2)
says that dzt is the sum of bdxt and a random
disturbance given by g
is a real constant
related to the behaviour of the mean of the stock prices index log return,
associated to the stochastic process of the stock prices index St
, t>0. Note that the stochastic
variance vt, t>0, is
assumed to be described by a mean-reverting process with speed c³0 and parameters q³0 and e³0, that is by equation (3). The stochastic differential equations (1), (3) are
known as Heston model [2]. Equation (2) has been
introduced to model the log-returns of the indices of suitable classes of hedge
funds (such as, for example, the long short equity class). In fact equation (2)
says that dzt is the sum of bdxt and a random
disturbance given by g![]() dWt3, where b and g
are real constants. If we interpret zt,
t>0, as the log-return at time t of the index of one of these classes of
hedge funds, xt, t>0, as the log-return at time t of the stock
prices index, for example the S&P500 index, and vt, t>0, as the
stochastic variance of xt,
t>0, equation (2) can be regarded as a reasonable translation in the
continuous time setting of the findings of the time series analysis presented
in [3] and the
system (1), (2), (3) can be interpreted
as a model to explain the dynamics of the log-return of the index of one of the
classes of hedge funds mentioned previously that uses the log-return of the S&P500 index and its
stochastic variance as explanatory variables. We remark that the models
proposed in [3] are discrete time models.
dWt3, where b and g
are real constants. If we interpret zt,
t>0, as the log-return at time t of the index of one of these classes of
hedge funds, xt, t>0, as the log-return at time t of the stock
prices index, for example the S&P500 index, and vt, t>0, as the
stochastic variance of xt,
t>0, equation (2) can be regarded as a reasonable translation in the
continuous time setting of the findings of the time series analysis presented
in [3] and the
system (1), (2), (3) can be interpreted
as a model to explain the dynamics of the log-return of the index of one of the
classes of hedge funds mentioned previously that uses the log-return of the S&P500 index and its
stochastic variance as explanatory variables. We remark that the models
proposed in [3] are discrete time models.
The equations (1), (2), (3) must be equipped with an initial condition,
that is:

Here ![]() ,
,![]() , and
, and ![]() denote random
variables concentrated with probability one in a point; for simplicity, we
continue to denote these points respectively with
denote random
variables concentrated with probability one in a point; for simplicity, we
continue to denote these points respectively with ![]() ,
,![]() , and
, and ![]() . We note that
. We note that ![]() ,
, ![]() , that is the log-returns of the stock prices index and of
the index of the hedge funds class at t=0, are
observable while
, that is the log-returns of the stock prices index and of
the index of the hedge funds class at t=0, are
observable while ![]() , that is the stochastic variance at t=0, cannot be observed.
The quantities
, that is the stochastic variance at t=0, cannot be observed.
The quantities ![]() , q, c, e, g, b and r1,2, r1,3, r2,3 are real constants and are the model
parameters that we want to estimate. Hence, the parameters and unknown initial
condition component of the model (1), (2), (3) that we want to estimate
are
, q, c, e, g, b and r1,2, r1,3, r2,3 are real constants and are the model
parameters that we want to estimate. Hence, the parameters and unknown initial
condition component of the model (1), (2), (3) that we want to estimate
are ![]() , q, c, e, g, b, r1,2, r1,3, r2,3 and
, q, c, e, g, b, r1,2, r1,3, r2,3 and ![]() . We assume that 2cq/e2 ³1, this assumption guarantees that
if
. We assume that 2cq/e2 ³1, this assumption guarantees that
if ![]() is positive with
probability one, vt, solution of
(3), (5) remains positive with probability one for
t>0.
is positive with
probability one, vt, solution of
(3), (5) remains positive with probability one for
t>0.
We suppose that at discrete times 0=t0<t1<t2<…<tn<tn+1
=+¥, the log-return of the stock prices index and the log-return of the
index of a special class of hedge funds are observed and let Ft= {(![]() ,
,![]() ) : ti £t}, t>0, be the set of the observations up
to time t>0 of the log-returns of the stock prices index xt and
of the log-returns of the index of the hedge funds, that is for i=1,2,...,n,
let
) : ti £t}, t>0, be the set of the observations up
to time t>0 of the log-returns of the stock prices index xt and
of the log-returns of the index of the hedge funds, that is for i=1,2,...,n,
let ![]() be the observation of
the log-return of the stock prices index and
be the observation of
the log-return of the stock prices index and
![]() be the observation of
the log-return of the hedge funds index at time t=ti . We assume
that the observations are error free, that is we assume
be the observation of
the log-return of the hedge funds index at time t=ti . We assume
that the observations are error free, that is we assume ![]() =
=![]() ,
, ![]() =
=![]() , i=0,1,…,n. Let
, i=0,1,…,n. Let ![]() be the vector of the
model parameters and of the initial stochastic variance, where the superscript T
denotes the transpose operator. We use the notation t0 =0 and F0={(
be the vector of the
model parameters and of the initial stochastic variance, where the superscript T
denotes the transpose operator. We use the notation t0 =0 and F0={(![]() )} to simplify the formulae that
follow.
)} to simplify the formulae that
follow.
3. Filtering problem
Let us
assume the vector Q known, we focus on the
problem of forecasting the state variables
from the observations previously described. This problem is a filtering
problem, where the stochastic differential equations (1), (2), (3) represent
the “state equations”,  and
and
 at time t0 is the initial condition and, for i=1,2,...,n,
(
at time t0 is the initial condition and, for i=1,2,...,n,
( ,
,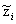 ) at time ti
represent the observations of the filtering problem. Note that in the filtering problem the initial stochastic variance
) at time ti
represent the observations of the filtering problem. Note that in the filtering problem the initial stochastic variance 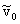 is known through the
knowledge of Q and that since
is known through the
knowledge of Q and that since 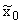 ,
, 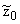 are observed in the filtering problem the initial condition
are observed in the filtering problem the initial condition
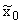 ,
, 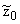 ,
,
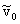 is known. The solution of this filtering problem is based on the knowledge of
the joint probability density function
is known. The solution of this filtering problem is based on the knowledge of
the joint probability density function 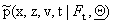 , (x,z,v)Î( -¥,+¥)
, (x,z,v)Î( -¥,+¥)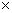 (-¥,+¥)
(-¥,+¥)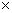 (0,+¥) , t>0, of the state
variables conditioned to the observations Ft, t>0, and to
the initial condition (4), (5), (6).
(0,+¥) , t>0, of the state
variables conditioned to the observations Ft, t>0, and to
the initial condition (4), (5), (6).
The joint probability density function ![]() , (x,z,v)Î (-¥,+¥)
, (x,z,v)Î (-¥,+¥)![]() (-¥,+¥)
(-¥,+¥)![]() (0, +¥) , t>0, of having xt=x, zt=z,
vt=v, t>0, conditioned to the observations Ft,
t>0, is solution of the following
equations [1] : for i=0,1,...,n:
(0, +¥) , t>0, of having xt=x, zt=z,
vt=v, t>0, conditioned to the observations Ft,
t>0, is solution of the following
equations [1] : for i=0,1,...,n:
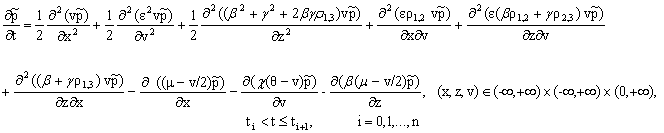 (7)
(7)
with initial condition: for i=0:
![]() =d
=d![]() d
d![]() d
d![]() , (x,z,v)Î( -¥,+¥)
, (x,z,v)Î( -¥,+¥)![]() (-¥,+¥)
(-¥,+¥)![]() (0,+¥) , t=t0, (8)
(0,+¥) , t=t0, (8)
and for i=1,2,...,n:
![]() =
=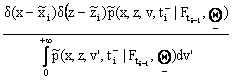 , (x,z,v)Î( -¥,+¥)
, (x,z,v)Î( -¥,+¥)![]() (-¥,+¥)
(-¥,+¥)![]() (0,+¥) , t=ti. (9)
(0,+¥) , t=ti. (9)
Once we know the joint probability density ![]() (x,z,v,t|Ft,Q), (x,z,v) Î (-¥,+¥)
(x,z,v,t|Ft,Q), (x,z,v) Î (-¥,+¥)![]() (-¥,+¥)
(-¥,+¥)![]() (0, +¥), t>0, we can forecast the values of the
random variables (xt, zt ,vt), t>0, conditioned
to the observations using the quantities
(0, +¥), t>0, we can forecast the values of the
random variables (xt, zt ,vt), t>0, conditioned
to the observations using the quantities
![]() given by:
given by:
![]() (10)
(10)
![]() (11)
(11)
![]()
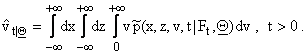 (12)
(12)
The quantities ![]() can be regarded as the
solution of the filtering problem.
can be regarded as the
solution of the filtering problem.
Let G(x,z,v,t,x',z’,v',t'|Q), (x,z,v), (x',z’,v') Î(-¥,+¥)![]() (-¥,+¥)
(-¥,+¥)![]() (0, +¥) ,
t>t'>0, be the fundamental solution of (7) whose expression is given in
[1].
(0, +¥) ,
t>t'>0, be the fundamental solution of (7) whose expression is given in
[1].
Using the function
G the solution of problem
(7), (8), (9) can be written as follows:
![]() =G(x,z,v,t,
=G(x,z,v,t,![]() ,
,![]() ,
,![]() ,
,![]() |
| ![]() ), (x,z,v)Î(-¥,+¥)
), (x,z,v)Î(-¥,+¥)![]() (-¥,+¥)
(-¥,+¥)![]() (0,+¥),
(0,+¥), ![]() <t
<t![]() , (13)
, (13)
and for i=1,2,…,n:
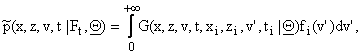
![]() (14)
(14)
where
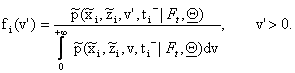 (15)
(15)
The evaluation of ![]() , (x,z,v)Î (-¥,+¥)
, (x,z,v)Î (-¥,+¥)![]() (-¥,+¥)
(-¥,+¥)![]() (0, +¥), t>0, for i=1,2,...,n, on a grid of N3
points in the (x,z,v) variables with a naïve quadrature procedure applied to
formula (14) using N quadrature nodes in each integration variable requires O(N6) complex
multiplications when N goes to infinity. In fact (14) due to the fact that the
fundamental solution G is obtained computing a two dimensional integral can be
regarded as a three dimensional integral. In [1] using:
(0, +¥), t>0, for i=1,2,...,n, on a grid of N3
points in the (x,z,v) variables with a naïve quadrature procedure applied to
formula (14) using N quadrature nodes in each integration variable requires O(N6) complex
multiplications when N goes to infinity. In fact (14) due to the fact that the
fundamental solution G is obtained computing a two dimensional integral can be
regarded as a three dimensional integral. In [1] using:
· a wavelet expansion [1],
[5] , [6] of the integral kernel appearing
in (14) and of the function (15),
· a truncation procedure that exploits
the sparsifying properties of the wavelet expansion,
· a suitable expansion in powers of a
time step and the Fast Fourier Transform
(FFT),
we reduce the computational cost of the
previous computation from O(N6) to N1O(N3log
N) complex multiplications when N goes to infinity, where N1 is
independent of N. Note that N1 is the number of the wavelet
functions remaining in the expansion of the integral kernel after the use of the
truncation procedure.
Using the estimates (10), (11), (12) we can
forecast the values of the log-return of the stock prices index xt, t>0, of the log-return of
the hedge funds class index zt, t>0, and of the stochastic variance vt,
t>0, coherently with the observations
Ft, t³0. The continuous update in time of ![]() is the “trajectory
tracking” of (1), (2), (3), (4), (5), (6). The continuous update in time of
is the “trajectory
tracking” of (1), (2), (3), (4), (5), (6). The continuous update in time of ![]() is the corresponding “variance
tracking”.
is the corresponding “variance
tracking”.
The quality of the forecasted values ![]() depends on the variance of the random variables xt,
zt vt, t>0,
conditioned to the observations, that is we can estimate the quality of the
estimates (10), (11), (12) computing respectively the quantities:
depends on the variance of the random variables xt,
zt vt, t>0,
conditioned to the observations, that is we can estimate the quality of the
estimates (10), (11), (12) computing respectively the quantities:
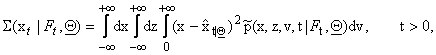 (16)
(16)
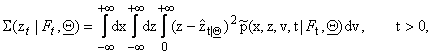 (17)
(17)
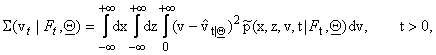 (18)
(18)
The estimates (10), (11), (12) are good, when
the variances (16), (17), (18) are small.
Click here to download a digital
movie showing the trajectory tracking.
Click here
to download a digital movie showing the
evolution in time of the integral with respect to x of the joint probability
density function conditioned to the observations obtained solving the filtering
problem. That is the digital movie shows the evolution in time of the function
D(z,v,t),  ,
,  , where D is defined as D(z,v,t)=
, where D is defined as D(z,v,t)= 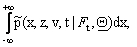
 ,
,  .
.
In the trajectory tracking shown in Figure 1
and in the digital movie showing the
trajectory tracking the solid line
represents the true trajectory made of the values (xt, zt
vt), tÎ[0,24/252.5], obtained computing numerically
for t > 0 with Euler method one trajectory of the
stochastic differential equations (1), (2), (3) with the initial condition (4), (5), (6)
![]() =0,
=0, ![]() =0, and
=0, and
![]() =0.5;
the dashed line represents the trajectory followed by the
forecasted values
=0.5;
the dashed line represents the trajectory followed by the
forecasted values ![]() tÎ[0,24/252.5], obtained solving the filtering problem
computing the integrals (10), (11), (12) and using the data shown in Table 1. The
squares and the asterisks indicate,
respectively, the values of (xt,
zt vt) and of
tÎ[0,24/252.5], obtained solving the filtering problem
computing the integrals (10), (11), (12) and using the data shown in Table 1. The
squares and the asterisks indicate,
respectively, the values of (xt,
zt vt) and of ![]() at the observation
times t=ti, i=0,1,...,5. We have chosen Q = (0.026, 5.94, 0.306, 0.01159,1,0.1,
-0.576,0,0, 0.5)T. We note that
b,
g,
r1,2, r1,3, r2,3 are adimensional quantities and that
at the observation
times t=ti, i=0,1,...,5. We have chosen Q = (0.026, 5.94, 0.306, 0.01159,1,0.1,
-0.576,0,0, 0.5)T. We note that
b,
g,
r1,2, r1,3, r2,3 are adimensional quantities and that ![]() , q, c, e,
, q, c, e,
![]() dimensionally are 1/time. We assume
that the components
dimensionally are 1/time. We assume
that the components ![]() , q, c, e,
, q, c, e,
![]() of the parameter vector Q are expressed in annualized unit, that is in
the unit 1/year. We use a “year” made of the average number of trading days per
year, that is made of 252.5 days, so that for example t=24/252.5 corresponds to the end
of the trading day number 24 of the regular year.
of the parameter vector Q are expressed in annualized unit, that is in
the unit 1/year. We use a “year” made of the average number of trading days per
year, that is made of 252.5 days, so that for example t=24/252.5 corresponds to the end
of the trading day number 24 of the regular year.
|
i |
ti |
|
|
|
0 |
0 |
0 |
0 |
|
1 |
4/252.5 |
-0.1046324981 |
-0.09423814923 |
|
2 |
8/252.5 |
-0.0389636566 |
-0.03170475035 |
|
3 |
12/252.5 |
-0.1106878449 |
-0.09375359522 |
|
4 |
16/252.5 |
0.01355863752 |
0.036249189791 |
|
5 |
20/252.5 |
0.04209650394 |
0.053437008036 |
Table 1. The data of the filtering problem
Below we show two figures (Figure 1 and Figure
2) that help the understanding of the quality of the estimates obtained solving
the filtering problem. We remind that Figure 1 shows the trajectory tracking
obtained as solution of the filtering problem. In particular the solid line
represents the
true trajectory made of the values (xt, zt
vt), tÎ[0,24/252.5], obtained computing with Euler method one
trajectory of the initial value problem (1), (2), (3), (4), (5), (6),
the dashed line represents the trajectory followed by the forecasted values
of ![]() , tÎ[0,24/252.5]. Figure 2 shows S(xt | Ft, Q), S(zt | Ft, Q), S(vt | Ft, Q) versus
time when tÎ[0,24/252.5]. In the figures the
time is expressed in days that is
, tÎ[0,24/252.5]. Figure 2 shows S(xt | Ft, Q), S(zt | Ft, Q), S(vt | Ft, Q) versus
time when tÎ[0,24/252.5]. In the figures the
time is expressed in days that is ![]() .
.
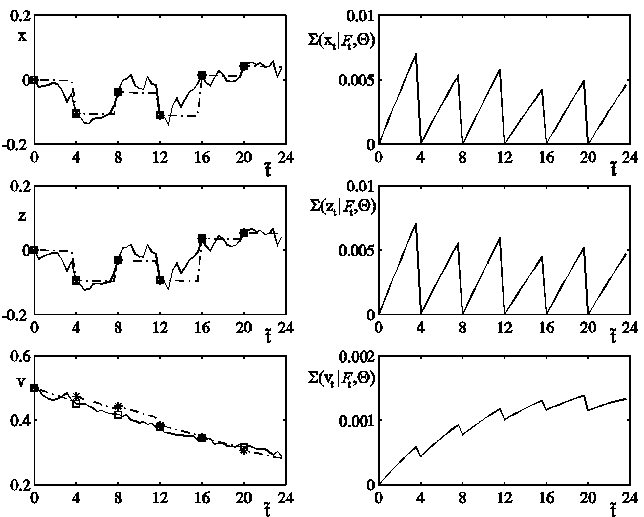
Figure 1. Tracking of xt, zt, vt versus ![]() Figure 2. S(xt|Ft ,Q), S(zt|Ft ,Q), S(vt|Ft ,Q) versus
Figure 2. S(xt|Ft ,Q), S(zt|Ft ,Q), S(vt|Ft ,Q) versus
![]()
In Section 3 we have assumed Q
known to solve the filtering problem but in real situations when the model (1), (2), (3) is used Q is
not known and it must be estimated from the knowledge of the observations. The
dynamics of the stochastic process (xt, zt vt), t>0, and of the estimates ![]() t>0, obtained from the solution of the filtering
problem, depend on the vector
t>0, obtained from the solution of the filtering
problem, depend on the vector ![]() Let
Let ![]() be the set of the admissible vectors Q.
be the set of the admissible vectors Q.
We solve the problem of estimating
the vector Q
from the observations using the maximum likelihood method. That is we search
the vector QÎM
that maximizes the following (log-)likelihood
function:
![]() (19)
(19)
Note that (19) represents the sum of
the logarithms of the integrals of the transition probability densities ![]() (xi+1,
zi+1,v,ti+1|Fti ,Q),
i=0,1,...,n-1. The function F(Q)
represents the (log-)likelihood of
the parameter vector Q given the observations Ft, t>0,
and the initial condition
(xi+1,
zi+1,v,ti+1|Fti ,Q),
i=0,1,...,n-1. The function F(Q)
represents the (log-)likelihood of
the parameter vector Q given the observations Ft, t>0,
and the initial condition ![]()
![]() at time t=t0.
at time t=t0.
In order to maximize the (log-)likelihood
function shown in (19), we use an iterative optimization procedure that
searches the maximum likelihood estimate Q* solution
of the maximization problem:
![]() (20)
(20)
starting from an initial guess Q0ÎM.
The iterative procedure that solves the
optimization problem (20) using Q0 as initial guess finds during the iterations
the admissible vectors Qk,, k=1,2,...,iter,
where iter is the maximum number of iterations allowed. The vectors Qk, k=0,1,…,iter, are such that F(Qk+1)³F(Qk), k=0,1,…,iter-1.
In the first numerical experiment we use as data of the estimation problem the same
data used for the filtering problem that is the data shown in Table 1. These
are synthetic data that were generated using
Q=Qtrue = (0.026, 5.94, 0.306,
0.01159,1,0.1 -0.576,0,0, 0.5)T. We choose as initial guess of the
optimization procedure the vector Q0=Qtrue(1+0.8¡), where
¡ has been sampled from 10-dimensional standard Gaussian variable with
independent components. We assume Q0ÎM if this is not the case
we discard it and we
sample
the 10 dimensional Gaussian variable again.
We fix
the maximum number of iterations allowed iter=100, we use the variable metric
steepest ascent method described in [1] as optimization
method to solve problem (20) and we use the following stopping criterion:
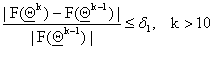 (21)
(21)
where d1 is a given tolerance. Choosing d1 =0.001 the variable metric steepest ascent procedure
stops at the iteration k=19, with Q19=(0.025,4.765,0.252,
0.011,0.96,0.106, -0.521, 0.071,-0.019,0.492)T and we have F(Q19) @ 23.54, F(Q0) @ 12.91, and F(Qtrue) @ 23.10 .
Click here
to download a digital movie showing the trajectory tracking for Q = Qk ÎM , k=0,1,2,…,19, obtained during the
iterative optimization procedure and the true trajectory corresponding to Q=Qtrue obtained integrating numerically (1), (2), (3), (4),
(5), (6).
The second experiment consists in analyzing a series of daily observations during a
period of two years, that is a series made of 505 observation times. Remind
that we have considered a “year” made of 252.5 trading days. We consider 505
observation times corresponding to 1010 observations ![]() ,
,![]() , i=0,1,…,504, where we have chosen t0=0, x0=
, i=0,1,…,504, where we have chosen t0=0, x0=![]() =0, z0=
=0, z0=![]() =0, v0=
=0, v0=![]() =0.5. The data are generated integrating numerically with Euler
method one trajectory of (1), (2), (3), (4), (5), (6) for two years period.
We choose the vector
=0.5. The data are generated integrating numerically with Euler
method one trajectory of (1), (2), (3), (4), (5), (6) for two years period.
We choose the vector ![]() of the stochastic differential
system that generates the data to be equal to the vector
of the stochastic differential
system that generates the data to be equal to the vector ![]() used in the previous
experiment in the first year of data (i.e. when t=ti , i=0,1,…,252)
and to the vector
used in the previous
experiment in the first year of data (i.e. when t=ti , i=0,1,…,252)
and to the vector ![]() in the second year of
data (i.e. when t=ti , i=253,254,…,504) where
in the second year of
data (i.e. when t=ti , i=253,254,…,504) where ![]() and
and ![]() are given by:
are given by: ![]() =(0.026,5.94,0.306,0.01159,1,0.1,
-0.576,0,0,0.5)T
,
=(0.026,5.94,0.306,0.01159,1,0.1,
-0.576,0,0,0.5)T
, ![]() =
(0.4,2,0.01,0.01,1,0.01,0.5,0,0,0.012)T.
=
(0.4,2,0.01,0.01,1,0.01,0.5,0,0,0.012)T.
Click
on the names to download the file
containing the observations ![]() (samplexx.txt)
,
(samplexx.txt)
,![]() (samplezz.txt), i=0,1,…,504.
(samplezz.txt), i=0,1,…,504.
We solve problem (20) using a time window made of 9
consecutive observation times corresponding to 18 observations. In particular
we divide the time interval [0,504/252.5] in 63 consecutive disjoint time windows containing 8 consecutive
observation times that is for j=0,1,…,62 the time values t=ti,j=t8j+i, i=1,2,…,8 belong to
the same time interval. Note that when considering the time window j (j³1) we use
the notation t0,j=t8j that is t0,j is the
last observation time of the time window
j-1. Note that 8´63=504 and
that the observation time t=t0 is not considered in the time windows considered above. The observation
time t=t 0 is associated to the first time window (j=0)
and we use the notation t0,0=t0. We solve problem
(20) using the observations made at 9 consecutive observation times that is given j using
![]() ,
,![]() , at time t=ti,j i=0,1,…,8, that is for j=0,1,…,62 the time values ti,j=t8j+i,
i=0,1,2,…,8 belong to the same time window.
We solve 63 problem
(20) starting from different initial guesses. In Figure 3 the diamond
represents the vector
, at time t=ti,j i=0,1,…,8, that is for j=0,1,…,62 the time values ti,j=t8j+i,
i=0,1,2,…,8 belong to the same time window.
We solve 63 problem
(20) starting from different initial guesses. In Figure 3 the diamond
represents the vector ![]() and the square represents the vector
and the square represents the vector ![]() . The unit
length in Figure 3 is
. The unit
length in Figure 3 is ![]() . The origin is the mid point of the segment that joins the points
. The origin is the mid point of the segment that joins the points
![]() and
and ![]() and the length of the segment that joins the
diamond and the square is proportional to the Euclidean norm of the vector
and the length of the segment that joins the
diamond and the square is proportional to the Euclidean norm of the vector ![]() -
- ![]() . The vector
determined solving problem (20) using the optimization procedure are
represented by stars. A point P=Q is plotted around
. The vector
determined solving problem (20) using the optimization procedure are
represented by stars. A point P=Q is plotted around ![]() when the quantity
when the quantity ![]() is smaller than the
quantity
is smaller than the
quantity ![]() , otherwise it is plotted around
, otherwise it is plotted around ![]() . The point
P is plotted on the left or on the right of the point that represents
. The point
P is plotted on the left or on the right of the point that represents ![]() or
or ![]() according with the sign of
according with the sign of ![]() , the eighth component of the
vector Q
that is
the estimated correlation coefficient
, the eighth component of the
vector Q
that is
the estimated correlation coefficient ![]() . Finally the difference of the abscissae of the point
. Finally the difference of the abscissae of the point ![]() and a point P=Q of its cluster
is
and a point P=Q of its cluster
is ![]() . A similar statement
holds for
. A similar statement
holds for ![]() and a point P on the cluster
associated to
and a point P on the cluster
associated to ![]() . We remind
that in Figure 3 the unit length is
. We remind
that in Figure 3 the unit length is ![]() .
.

Figure 3: Reconstruction of the parameter vectors ![]() ,
, ![]()
Click here
to download a digital movie showing the
points determined solving the 63 problem
(20) described above as a function of the time window of the observations.
Figure
3 and the digital movie that shows the solution of the 63 problem (20) show
that the points obtained solving problem (20) are concentrated on two disjoint
segments one on the left and one on the right of the origin and that they form two
disjoint clusters, that is, the solution of the 63 problems (20) corresponding
to the time windows described previously
shows that two sets of parameters seem to generate the data studied.
This is really the case. Moreover as expected the points of the cluster around Q2 are those obtained by the analysis
of the observations made in the second year.
L.Fatone,
F.Mariani, M.C.Recchioni, F.Zirilli, Maximum
likelihood estimation of the parameters of system of stochastic
differential equations that models the
returns
a of the index of some
S.L.Heston, A closed-form solution
for options with stochastic volatility with applications to bond and currency
options , Review of Financial Studies, 6, 327-343 (1993).
P. Pillonel, L. Solanet, Predictability in hedge fund index returns
and its application in fund of hedge funds style allocation, Master's Thesis
in Banking and Finance at Université de
Lausanne, Hautes Etudes Commerciales (HEC), (2006).
L.Fatone, M.C.Recchioni, F.Zirilli,
Wavelet Bases Made of Piecewise Polynomial Functions:
Theory and Applications, Applied Mathematics, 2, 196-216 (2011).
L.Fatone, G.Rao, M.C.Recchioni,
F.Zirilli, High performance algorithms based on a new wavelet expansion for
time dependent acoustic obstacle scattering, Communications in
Computational Physics, 2(6), 1139-1173 (2007).
F.Mariani, G.Pacelli, F.Zirilli, Maximum
likelihood estimation of the Heston stochastic volatility model using asset and
option prices: an application of nonlinear filtering theory, Optimization Letters, 2, 177-222 (2008).
The FORTRAN code distributed in this website
computes the solution of the estimation problem (20) using the formulae
outlined in Sections 3 and 4 and derived in [1] . The data
of the estimation problem are those described in Section 4 and must be provided
by the user. The FORTRAN code consists of two programs.
The first program preproc.f90 reads and writes on appropriate files the
data given by the user, initializes the parameter vector Q0 and computes the number of wavelet coefficients needed after the
truncation procedure in order to approximate satisfactorily the integral kernel
contained in (14) associated to the initial guess Q0.
click here to download preproc.f90
The second program estimate.f90 starting from the initial guess Q0 generates a sequence of admissible vectors Qk, k=1,2,…,iter, using a variable
metric steepest ascent optimization procedure.
click here to download estimate.f90